Inscription / Connexion Nouveau Sujet
Factorisation blocage
Bonsoir,
Je dois faire un exercice pour la rentrée des vacances d'hiver, mais dans cet exercice je bloque sur une inéquation.
Je vous met l'énoncé : Résoudre les inéquations après avoir factorisé le premier membre en produit de fonctions affines.
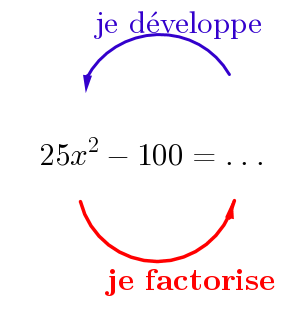
Etant donné que j'ai réussi les autres inéquations, j'aimerais que vous m'aidez pour la dernière qui est : x*(25x²-100)>0
Je ne sais pas comment résoudre celle-ci..
Merci d'avance pour votre aide,
Bonjour.
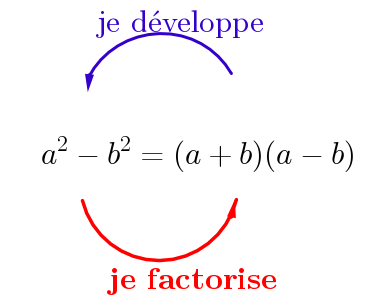
25x² - 100 = différence de deux carrés.....a²-b²=.....
un tableau de signes et on trouve la solution.
malou edit
une fois que tu auras factorisé, tu feras un tableau de signes, il y a des exemples ici : ![]() cinq exercices utilisant les tableaux de signes
cinq exercices utilisant les tableaux de signes
Pour résoudre toi inequation, Il y a une identité remarquable à faire ressortir a^2-b^2=(a-b) (a+b)
****message modéré***balancer une solution ce n'est pas aider****
Alors je pense avoir compris, mais dites moi si ma réponse est correcte ou pas...
x*(25x²-100)>0
x*(5x-10)(5x+10)=0
sois x = 0
sois : 5x-10=0
5x=10
x = 10/5= 2
sois : 5x+10=0
5x=-10
x = -10/5=-2
donc : S={-2;0;2}
alors attends, oui pour ...=0
mais il te reste maintenant à faire ton tableau de signes pour répondre à l'inéquation
oui, ok
et on te demande de donner les x pour que ce produit soit strictement positif
et tu réponds alors ....
Et j'ai une question.. pourquoi aux inéquations on remplace les signes " < et > " par le signe "=" alors que pourtant j'ai le souvenir que pour les inéquations on change le sens de l'inéquation si on divise ou multiplie par un nombre négatif non ?
les inéquations restent avec les signes < , > et  ,
, 
mais c'est vrai que pour trouver les valeurs à mettre dans ton tableau, tu résous d'abord ....= 0
non, pas du tout
le produit est strictement positif lorsqu'à la dernière ligne de ton tableau, tu vois des " + "
ta solution sera écrite sous la forme d'une réunion de deux intervalles
essaie
alors là tu as écrit des intervalles fermés, or nous, nous ne voulons pas des extrémités, donc tu vas devoir ouvrir tes intervalles
remarque : en + ou - l'infini, de toutes façons, c'est par principe ouvert
ensuite tu confonds l'intersection  et la réunion
et la réunion 
nous, nous voulons aujourd'hui la réunion
tu réécris....






