Bonjour

Bijective de quoi dans quoi?

Alors grossièrement:

u=y/x² et v=xy

y=ux², donc v=ux³ et enfin



Tu es sur(e) que c'était la question posée?

En fait je dois montrer que f(x,y) = (y/(x^2), xy) est un C^1 difféomorphisme de E dans F ou
E={ (x,y) de R^2 tels que (x^2)<y<2(x^2) et (1/x)<y<(2/x) } et F est à déterminer.

C'est bien ce qu'il me semblait! Bon, avec mes formules au moins tu trouveras F. Attention, tu as des contraintes fortes!

x doit être différent de 0 mais après je dois m'aider de E ou pas? F= R\{0} * R?
En tout cas merci pour ton aide Camélia.

Si (x,y) est dans E, et si (u,v)=f(x,y), tu as 1 < u < 2 et 1 < v < 2. Essaye de montrer que F=f(E)=[1,2][1,2]

Après avoir fait le graphe de E j'ai trouvé que: 2^(-1/3)<x<2^1/3 et 1<y<2, c'est juste?

Je ne comprends pas... E est donné!

oui E={ (x,y) de R^2 tels que (x^2)<y<2(x^2) et (1/x)<y<(2/x) }

Oui, j'ai vu, je t'ai même donné F, c'est ton post de 16:15 que je ne comprends pas! Voilà à quoi ça ressemble: E est le "carré" délimité par les quatre courbes:

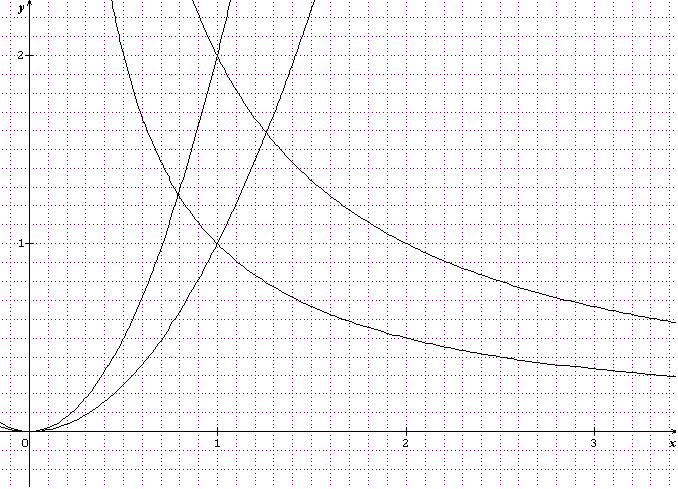
Oui c'est ça que j'ai trouvé mais je ne comprends pas comment tu trouves F.
Moi je trouve F= [2^(-2/3),2*2^-2/3]*[2^(-1/3),2*2^(1/3)].

Si et si on a bien 1 < u < 2 ? non?

Si et si on a bien 1 < v < 2, non?

Réciproquement si et si on pose et on a donc et donc ce qui montre que et qu'on a bien trouvé f^-1.

Ah oui, merci beaucoup.
J'ai une autre question est-ce que la convergence normale entraine la convergence uniforme?

Oui, bien sur.

Merci pour ton aide Camélia.