Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieur AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau école ingénieur
Partager :

Fonction erg - Intégrales

Posté par
Yalika 14-06-13 à 09:50

Bonjour,

Je galère un peu sur une section d'un dossier sur la fonction erf . (erreur de Gauss).

En mathématique, les intégrales servent à définir de nouvelles fonctions ; par exemple ≪ la
fonction d'erreur ≫ erf, omniprésente en probabilités.

erf(x)  ~\stackrel{\textrm{déf}}{=}~  \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} dt

Ensuite on me demande :

1) Quel(s) sens peut-on donner à cette intégrale : Newton? Riemann? Kursweil & Henstock ?

2) Calculer la dérivée de erf. Comparer avec Sage.
(Donc là j'ai dit que ça découlait directement de la définition de la fonction et que c'était égal à $Erf'(x)=\frac{2}{\sqrt{\pi}} e^{-t^2} dt $


3) Calculer des valeurs approchées de $erf(1)$ par des sommes de Riemann, par la méthode des trapèzes. Comparer avec Sage.

4) Montrer que $\ds \lim_{x\rightarrow +\infty} erf(x) = 1$.

5 ) On considère une variable aléatoire réelle $X$ suivant une loi de Gauss de moyenne $m$ et de variance $\sigma^2$, c'est à dire de fonction de répartition donnée par

(voir image ci-dessous)

Exprimer $F_X$ à l'aide de la fonction $erf$.

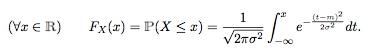
Fonction erg - Intégrales

Posté par
DOMOREAFonction erg - Intégrales 14-06-13 à 10:38

Bonjour,
Tu peux revoir ta question 2 ....  ta dérivée ?  t?    dt ?
Pour la Q5 Commence par faire dans erg(f(x) le changement de variable t=\frac{u}{\sqrt{2}}
Puis tu te souviendras que \frac{1}{\sqrt{2\pi}}\int^0_{-\infty}e^{-t^2/2}dt=1/2

Posté par
DOMOREAFonction erg - Intégrales 14-06-13 à 10:40

Re
er et non pas erg

Posté par
Yalikare : Fonction erg - Intégrales 14-06-13 à 10:54

Ah oui ! c'est dans le copier/coller que j'ai oublié d'enlever le "dt". C'est bien ça, il suffit de l'enlever non ?
Et oui, l'ordinateur corrige toujours erf en erg automatiquement...

Je te poste la réponse que j'ai rédigé :

La loi normale de Gauss s'exprime de la manière suivante :

P(t)=\frac{1}{2\sqrt{\pi}} \int_{-\infty}^x e^{- \frac{(t)^2}{2}} dt.
On effectue un changement de variable $t= \frac{u}{\sqrt{2}}$ d'où
P(t)=\frac{1}{2} \cdot (1+erf(\frac{t}{\sqrt{2}}))

Est-ce que tu penses qu'en disant ça ça suffit ou il faudrait que je détaille ?

Pour les questions 1) et 4), je suis aussi vraiment paumée, sur internet je trouve :

On ne peut pas obtenir l'intégrale de cette dernière avec Newton, dans la mesure ou la fonction $e^{-t^2}$ n'a pas de primitive exprimable avec des fonctions élémentaires. Il convient donc d'utiliser des méthodes de calculs numériques approchés.

Mais ça me paraît bizarre non ? Et après je ne sais pas dire si elle est R-intégrable ou seulement KH intégrable. Je pense qu'il y a pas besoin de démonstration, mais seulement d'avoir compris, ce qui n'est pas le cas

Posté par
miltonre : Fonction erg - Intégrales 14-06-13 à 11:06

salut
1) Reiman impropre convergente donc aussi HK (quoi que dans HK impropre n'est pas vraiment utile)
2)la methode  la plus rapide est de considerer \large \int_{\mathbb{R}^2}e^{-\frac{x^2+y^2}{2}}dxdy et faire un changement en coordonnées polaire en identifiant \mathbb{R}^2 à \lim_{r\to\infty}D(O,r)

Posté par
Yalikare : Fonction erg - Intégrales 14-06-13 à 11:24

Oulla, je suis en Bac+1 donc la méthode avec les coordonnées  on a vraiment pas du tout vu ça

Tu peux expliquer ce que ça veut dire "impropre convergente" ?
Ce que j'ai trouvé sur l'intégrale de Newton, c'est correct ?

Posté par
DOMOREAFonction erg - Intégrales 14-06-13 à 14:12

RE
Attention Dans P(t) c'est \sqrt{(2\pi)} et non pas 2\sqrt\pi=

Posté par
Yalikare : Fonction erg - Intégrales 15-06-13 à 13:01

Ah oui ! C'est noté ! J'ai modifié ça.

Mais donc, elle est intégrable au sens de N, R ou KH cette fonction ?

Après pour la question 3) j'ai une copine qui m'a envoyé sa réponse que j'ai du mal à comprendre, et je ne sais pas si c'est juste (je l'ai mise en image jointe).

4) ensuite pour la limite, je n'ai aucune idée de comment m'y prendre, c'est la première fois que je suis confrontée à une limite où c'est la borne d'une intégrale qui tend vers +oo.

Fonction erg - Intégrales

Posté par
miltonre : Fonction erg - Intégrales 15-06-13 à 13:44

elle est R et donc HK.
je crois que tu as oublié la hateur \frac{1}{n} dans la somme ;si non ca colle.
pour le 4) j'ai un vaa voir ici http://www.gecif.net/articles/mathematiques/integrales_particulieres/.
un conseil ,c'est pas tres conseillé de faire plusieur truc en mem temps,mais bon ....

Posté par
Yalikare : Fonction erg - Intégrales 15-06-13 à 15:32

Oui, je sais, j'ai un exercice sur Dir et un autre sur erf, mais en fait on est 2 à travailler en binôme et on poste ça sur le même compte du forum

Je ne comprends toujours pas comment calculer ça, même avec le site. Enfin, comment l'expliquer, parce que c'est plutôt ça que je dois faire, expliquer ce que j'ai compris Et vu que j'ai pas compris, bien... voilà le problème.

Pour la question 5), j'ai refait le développement et pour l'instant j'en suis à là (voir image jointe). Mais je ne sais pas vraiment comment m'y prendre pour faire mon changement de variable, ni quand...

Posté par
Yalikare : Fonction erg - Intégrales 16-06-13 à 11:06

Je viens de me rendre compte que je n'avais pas mis la piece jointe en image, donc normal j'ai pas de réponse

Posté par
Yalikare : Fonction erg - Intégrales 16-06-13 à 11:06

Mince mais c'est parce qu'il faut faire "attacher"

Fonction erg - Intégrales


Rechercher
Menu
Espace membre
23 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1734 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !