Inscription / Connexion Nouveau Sujet
fonction et interprétation graphique niveau seconde
Bonjour j'ai un devoir maison à faire pour les vacance mais j'ai oublier mes propriété donc j'avoue que je bloque j'aimerais que vous puissiez m'aider avec des explication merci
On considère les fonctions f et g définies sur ]- l'infinie;+ l'infinie[ par f(x)=18-2x² et g(x)=2x+6
On appelle C la courbe représentative de f .
1) Résoudre l'équation f (x) = 0 et interpréter graphiquement les solutions.
2)
a) Calculer l'expression de g ( x ) - f( x )
b) Montrer que 2x²+2x-12=(2x+6)(x-2)
c) Résoudre f ( x ) = g ( x ) et interpréter graphiquement ces solutions.
3) a ) Déterminer le signe du produit (2x + 6)(x-2)
b) En déduire les solutions de l'inéquation g(x) plus petit ou egale à f (x) et interpréter
graphiquement ces solutions.
Bonjour
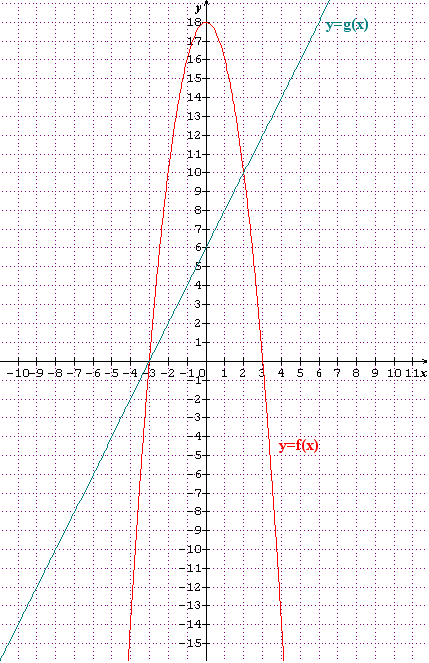
un graphique pr t'aider à comprendre
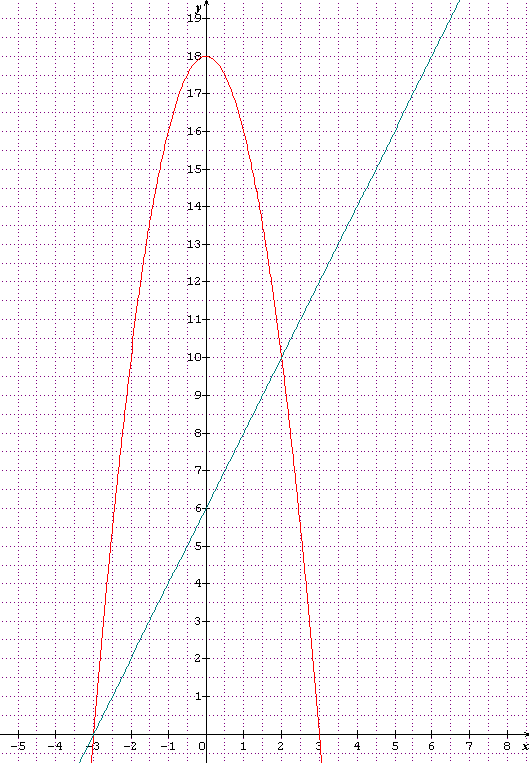
f(x) = 0 
18-2x² = 0 2x² = 18 x² = 9
Dc x = -3 OU x = 3, ce que confirme le graphique
Q2a : g(x)-f(x) = 2x+6-18-2x² = 2x²+2x-12 = (2x+6)(x-2), ce qu'on vérifie en développant
Q2c
f(x) = g(x) 18-2x² = 2x+6 2(9-x²) = 2(x+3)
sachant que 9-x² peut s'écrire : (3-x).(3+x),
cela revient à résoudre (x+3).(3-x) = x+3.
ce qui revient à poser : (x+3).(3-x)-(x+3) = 0 (x+3).[(3-x)-1] = 0 (x+3).(2-x) = 0
Pr qu'un produit de facteurs soit nul, il faut et il suffit que l'un des facteurs soit nuls, ce qui est vérifié pr x = - 3 OU x = 2, valeurs qui sont bien les abscisses des points d'intersection des courbes représentatives de f et de g.
D'accord ?
A ta disposition si tu as des questions.
Q3a
faire un tb de signes, comme ceci :
Q3b
g(x) 
f((x)
g(x) - f(x) 0
(2x+6)(x-2) 0
D'après le tb de signes, l'ensemble des solutions de l'onéquation est S = [-3;2]
ce qui se vérifie graphiquemen, on voit qu'entre les points d'abscisse x=-3 et x = 2, et uniquement sur cet intervalle, l'ordonnée qui correspond à g(x) est à celle correspondant à f(x).
Annuler
connectez vous