Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonction ExponentielleTopics traitant de Fonction Exponentielle [tout]Lister tous les topics de mathématiques

1 2 +

Niveau terminale
Partager :

fonction exponentielle

Posté par
moussolony 13-02-20 à 01:44

Bonjour

Le plan est muni d un repéré orthonormé (o,i,j) ,unité graphique : 2cm.
On considéré la fonction f de R dans R définie par: f(x)=xe^{\frac{1}{x+1}}
Si x différent de -1
f(-1)=0
C désigné la courbe représentative de f dans le repéré (0 ,i,j)
Partie A
On donne la fonction g de R vers R définie par: g(x)=1-\frac{x}{x+1}e^{\frac{1}{x+1}}
1/ calculer les limites de g en + infini et - infini

2/ étudier le sens de variation de g
3. Trouver le signe de g(x) suivant les valeurs de x
Partie B
1/ calculer les limites de f en + infini et en - infini
2. / a/ étudier la continuité de f en -1
b/ étudier la dérivabilité de f a gauche en -1
3/a/ étudier le sens de variation
de f en -1
b/ dresser le tableau de variation de f.
4/a/ vérifier que la droite (T): y=ex  , est tangente a c au point O.
b/ étudier la position de (c) par rapport a (T)
5a/ démontrer que la droite (D): y=x+1  , est asymptote a (c) en + infini et en - infini
b/ étudier la position relative de c et D .(on pourra utiliser la partie a)
6/ construire (c) avec soin.

Réponse
Question 1
En + infini
Lim g(x)=lim 1-(x)/(x+1)*e^{1/x+1)
Lim g(x)=0

En - infini
Lim g(x)=0
Question 2

g'(x)=é^{\frac{1}{x+1}}-\frac{x}{(x+1)^3}
Comme e^(1/x+1)>0 ,
J aimerais savoir si le signe de g'(x) dépend du signe x/(x+1)^3

Posté par
Zormuchere : fonction exponentielle 13-02-20 à 01:51

Bonsoir
ton g' est faux

Posté par
moussolonyre : fonction exponentielle 13-02-20 à 01:57

Pourquoi c est faux

Posté par
moussolonyre : fonction exponentielle 13-02-20 à 02:02

g'(x)=-e^{\frac{1}{x+1}}+\frac{x}{(x+1)^3}

Posté par
moussolonyre : fonction exponentielle 13-02-20 à 02:03

C est correcte maintenant

Posté par
heklare : fonction exponentielle 13-02-20 à 08:46

Bonjour

Non

g(x)=1-\dfrac{x}{x+1}\text{e}^{\frac{1}{x+1}}

u(x)=\dfrac{x}{x+1} \qquad u'(x)=\dfrac{1}{(x+1)^2}

v(x)=\text{e}^{\frac{1}{x+1}}\ ;\ v'(x)=-\dfrac{1}{(x+1)^2}\text{e}^{\frac{1}{(x+1]}


g'(x)=-\left(\dfrac{1}{(1+x)^2}\text{e}^{\frac{1}{x+1}}\left(1-\dfrac{x}{x+1}\right)\right)

à simplifier la dernière parenthèse d'abord

Posté par
moussolonyre : fonction exponentielle 18-02-20 à 11:48

Question 2
Pour tout nombre reel x,
e^(1/x+1)>0 et (1+x)^2>0
-(e^(1/x+1)/(1+x^2)<0
Étudions le signe (-2x)/(x+1)
Pour x appartement]- infini,-1[ U]0,+infini[, (-2x)/(x+1)<0
Pour x appartement ]-1,0[, (-2x)/(x+1)>0
Sens de variation
Pour x appartenant ]- infini,-1[ U]0,+infini[ ,g'(x)<0, donc g est strictement décroissant
Pour x appartenant a ]-1,0[ , donc g est strictement croissant

Posté par
heklare : fonction exponentielle 18-02-20 à 12:08

g'(x)=-\dfrac{\text{e}^{\frac{1}{1+x}} }{(x+1)^3}

g'(x) est donc du signe de -(1+x)

D'où vient 2x/(x+1)

Posté par
moussolonyre : fonction exponentielle 18-02-20 à 12:09

Est ce que c exact

Posté par
moussolonyre : fonction exponentielle 18-02-20 à 12:14

Pourquoi g '(x) est du signe -(1+x)

Posté par
heklare : fonction exponentielle 18-02-20 à 12:41

g'(x)=-\dfrac{1}{x+1}\left(\dfrac{\text{e}^{\frac{1}{x+1}}}{(x+1)^2}\right)

La grande parenthèse est strictement positive  il ne reste donc que -(x+1) dont le signe dépend des valeurs de x

Je ne peux répondre car je ne sais d'où sort 2x/(x+1)

Posté par
moussolonyre : fonction exponentielle 18-02-20 à 12:44

Question 2
Pour x appartenant]- infini,-1[, g'(x)>0, donc g est strictement croissant
Pour x appartenant]-1,+infini[ ,donc g est strictement décroissant.

Posté par
moussolonyre : fonction exponentielle 18-02-20 à 12:46

En concernant 2x/x+1
C est une faute de frappe

Posté par
moussolonyre : fonction exponentielle 18-02-20 à 12:55

Question 3
J ai fait le tableau de variation.mais
je n arrive pas calculer g(-1) parce que au trouve zéro au dénominateur

Posté par
heklare : fonction exponentielle 18-02-20 à 13:20

normal non définie  en -1 donc double barre dans le tableau

Posté par
moussolonyre : fonction exponentielle 18-02-20 à 13:27

Si je comprends très ,je dois calculer la limite a gauche et a droite de -1

Posté par
heklare : fonction exponentielle 18-02-20 à 13:30

Non pas obligatoirement on vous l'aurait demandé explicitement  ce qui importe est le signe de g

Posté par
moussolonyre : fonction exponentielle 18-02-20 à 13:38

OK
Voici ma proposition
Comme  g est strictement croissant sur ]-infini,-1[
Pour x appartenant]- infini,-1[ , g(x)>0
De même
Pour x appartenant]-1, + infini[
g(x)<0

Posté par
heklare : fonction exponentielle 18-02-20 à 14:21

g est croissante sur ]-\infty~;~-1[  lim en -\infty 0 donc g positive

g est décroissante sur ]-1~;~+\infty [ lim en +\infty 0 donc g positive

Posté par
moussolonyre : fonction exponentielle 18-02-20 à 14:37

Partie B
Question 1
En + infini
Lim x=+ infini et lim e(1/x+1)=1
Lim f(x)= + infini
En - infini
Lim x =-infini et lim e(1/x+1)=1

Question 2
Calculons la limite en -1
Lim x=-1
Je n arrive pas a calculer la limite de
e(1/x+1) car je trouve zéro au dénominateur

Posté par
heklare : fonction exponentielle 18-02-20 à 15:07

Illustration  de \mathcal{C}_g
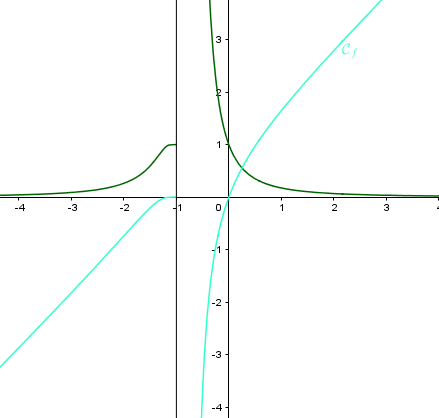
fonction exponentielle
et en vert  celle de f

Il faut conclure  +\infty en +\infty et -\infty en -\infty


Vous avez déjà vu ce genre de situation en seconde  comportement de la fonction inverse en 0

Posté par
moussolonyre : fonction exponentielle 18-02-20 à 23:48

Bonsoir
Non, je n ai jamais vu ce genre de situation. Comment vous avez trouvé ces limites sans le calcul

Posté par
heklare : fonction exponentielle 19-02-20 à 08:22

Quelles limites ?

\displaystyle  \lim_{x\to 0+}\dfrac{1}{x}=+\infty

Dans le cours vous devez avoir si f tend vers \ell et g tend vers 0 alors \frac{f}{g} tend vers \pm\infty selon la règle des signes

Posté par
moussolonyre : fonction exponentielle 19-02-20 à 17:47

Ok, si je comprends très bien
g(x) et f(x) sont inverse

Posté par
heklare : fonction exponentielle 19-02-20 à 18:16

Pourquoi dites-vous cela ?

J'ai parlé de la fonction inverse pour que vous vous souveniez de la courbe de x\mapsto\dfrac{1}{x}

en ne considérant que les positifs  tend vers +\infty quand x tend vers 0 et vers 0 quand x tend vers +\infty On ne parlait pas de limite

Posté par
moussolonyre : fonction exponentielle 19-02-20 à 18:36

Ok
Question 1a
Cette question est terminée alors
Question 2a
Calculons la limite en 1
Lim f(x)=lim xe^(1/x+1)
Posons X=1/x+1
f(x)=(1/X-1)e^x
Lorsque x gens vers -1 , X tends vers - infini
La limite en - infini
Lim (1/X-1)e^X=0

En définitive
La limite de f en -1
Lim f(x)=0
C est bon

Posté par
heklare : fonction exponentielle 19-02-20 à 19:26

il faut distinguer à droite et à gauche

\displaystyle \lim_{\substack{x\to -1\\x>-1}}\dfrac{1}{x+1}=+\infty

donc à droite -\infty et à gauche 0

Posté par
moussolonyre : fonction exponentielle 20-02-20 à 01:49

Bonjour
Question 2a
La limite à droite est différent de la limite a gauche .donc f n est pas continue en -1

Posté par
moussolonyre : fonction exponentielle 20-02-20 à 01:56

Question 2b
\frac{f(x)-f(-1)}{(x+1)}=\frac{xe^{\frac{1}{x+1}}}{x+1}
La limite a gauche de 1, j
Le numérateur tends vers 0 et le denominateur ,je trouve zero au dénominateur

Posté par
heklare : fonction exponentielle 20-02-20 à 08:39

X=\dfrac{1}{x+1}

\dfrac{f(x)-f(-1)}{x+1}=\dfrac{x\text{e}^{\frac{1}{x+1}}}{x+1}=x\dfrac{\text{e}^{\frac{1}{x+1}}}{x+1}=\left(\dfrac{1}{X}-1\right)\dfrac{\text{e}^X}{X}

\displaystyle \lim_{\substack {x\to-1\\x<-1}} X=-\infty\qquad \lim_{X\to -\infty} \dfrac{\text{e}^X}{X}=0 \qquad \lim_{X\to-\infty}\dfrac{1}{X}-1=-1

D'où la conclusion

Posté par
heklare : fonction exponentielle 20-02-20 à 08:46

Citation :
/a/ étudier le sens de variation de f en -1


Il n'y a pas de variation en un point  mais sur un intervalle.

Revoir le texte.

Posté par
moussolonyre : fonction exponentielle 20-02-20 à 09:08

Question 2b
Comme la limite tend vers + infini
Donc f n est pas dérivable en -1

Posté par
moussolonyre : fonction exponentielle 20-02-20 à 09:10

C est plutôt
3a/ étudier le sens de variation de f

Posté par
alb12re : fonction exponentielle 20-02-20 à 09:15

salut, presque le meme exercice ici fonction exponentielle

Posté par
heklare : fonction exponentielle 20-02-20 à 09:30

Limite finie   0 \times  -1=0 donc dérivable à gauche en -1

Posté par
moussolonyre : fonction exponentielle 20-02-20 à 11:36

Question 3a
f'(x)=e^{\frac{1}{x+1}}-x(\frac{e^{\frac{1}{x+1}}}{(x+1)^2}
Le signe de f'(x) est donc du signe de -x
Pour x appartenant]- infini,0[, f'(x)>0, donc f est strictement croissant
Pour x appartenant ] 0,+ infini[, f'(x)<0, donc f est strictement décroissant

Posté par
heklare : fonction exponentielle 20-02-20 à 12:09

On connaît le signe d'un produit pas celui d'une somme

f'(x)=\text{e}^{\frac{1}{x+1}}-\dfrac{x}{(x+1)^2}\text{e}^{\frac{1}{x+1}}

f'(x)=\text{e}^{\frac{1}{x+1}}\left(1-\dfrac{x}{(x+1)^2}\right)

f'(x)=\dfrac{\text{e}^{\frac{1}{x+1}}}{(x+1)^2}\left((x+1)^2-x\right)

pour tout x\in\R\setminus\{-1\},\  f'(x)>0

Ne pas oublier x\not=-1


Remarque : vous aviez le dessin de la courbe  18/02/2020 15:07

Posté par
moussolonyre : fonction exponentielle 20-02-20 à 12:36

Ok,mais
e^(1/x+1)/(x+1)^2 >0,et (x+1)^2>0
Pourquoi le signe f'(x) n est pas celui de x

Posté par
heklare : fonction exponentielle 20-02-20 à 12:55

f'(x)=\dfrac{\text{e}^{\frac{1}{x+1}}}{(x+1)^2}\left((x+1)^2-x\right)=\dfrac{\text{e}^{\frac{1}{x+1}}}{(x+1)^2}\left(x^2+x+1\right)

il n'y a que des termes strictement positifs

x n'est pas en facteur dans f'(x)

Posté par
alb12re : fonction exponentielle 20-02-20 à 18:27

Pour celles et ceux qui se perdraient dans tous ces calculs,
petite session Xcas projetable en classe lors du corrige/td

Posté par
moussolonyre : fonction exponentielle 23-02-20 à 19:00

Question 4a/
f(x)-ex=xe^{1/x+1)-ex
f(x)-ex=x(e^(1/x+1)-e)
Je suis bloqué

Posté par
heklare : fonction exponentielle 23-02-20 à 19:42

Que voulez-vous faire ?  le signe de ceci

signe d'un produit

\text{e}^{\frac{1}{x+1}}-\text{e} >0 \iff  \text{e}^{\frac{1}{x+1}}>\text{e}^1  

Posté par
moussolonyre : fonction exponentielle 23-02-20 à 22:21

Bonsoir
On a
e^(1/x+1)-e^x>0
Donc
f(x)-ex>0
f(x)>ex
D où la courbe est au dessus de la droite

Posté par
alb12re : fonction exponentielle 23-02-20 à 22:29

il faut resoudre par le calcul cette inequation voir 19h42

Posté par
moussolonyre : fonction exponentielle 23-02-20 à 22:33

On aura donc
1/x+1>1
x>0

Posté par
alb12re : fonction exponentielle 23-02-20 à 22:38

non tout dans un membre et signe du quotient

Posté par
moussolonyre : fonction exponentielle 24-02-20 à 00:11

On aura donc
-x/x+1>0
Pour x appartenant]-infini,-1[U]0,+ infini[, -x/x+1>0
Pour x appartenant] -1,0[ ,-x/x+1<0

Posté par
heklare : fonction exponentielle 24-02-20 à 08:35

Non

un trinôme est du signe de a sauf pour les valeurs comprises entre les racines donc

si x\in]-1~;~0[, \quad \dfrac{-x}{x+1}>0 et strictement négatif ailleurs

Ce n'est qu'une partie du produit dont vous cherchez le signe

Posté par
moussolonyre : fonction exponentielle 24-02-20 à 16:09

Voici ma proposition
Pour x appartenant]- infini,-1[ , la courbe est au dessus de la tangente
Pour x appartenant]-1,0[U]0,+ infini[, la courbe est en dessous de la tangente

Posté par
alb12re : fonction exponentielle 24-02-20 à 16:14

c'est juste

1 2 +


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1706 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !