Niveau Maths sup

Fonction logarithme

Posté par
CloudNine 19-01-17 à 20:01

Bonsoir,
Je suis bloqué à la question 2, 3, 5et 6.

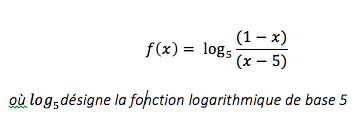
Fonction logarithme

1) Donner le domaine de définition Df de f
1 < x < 5

2) Calculer les limites aux bord sur Df. Conclure
$\lim_{x->5} f(x) = +oo$
$\lim_{x->1} f(x) = -oo$

3) Etudier la dérivabilité d sur son domaine de définition
Continuité puis dérivabilité en 1 et 5.
f(1) = log5(1)
f(5) = log5(0)
Je suis bloqué pour le calcul de la limite du taux d'accroissement en 1 et 5.

4) Etudier les variations de f
J'ai trouvé:
f'(x) = -4/( (x-5)(x-1)*log5 )

5) Déterminer les valeurs de x telles que f(x) ≥ 1

6) Montrer que f est bijective et déterminer l'application réciproque f^-1
Soit une fonction, f de E vers F est bijective si et seulement si tout élément de F possède exactement un antécédent dans E (ce qui équivaut à dire que f est à la fois injective et surjective).

Merci d'avance pour vos aides,

Posté par re : Fonction logarithme 19-01-17 à 22:02

Bonjour CloudNine

Une fois que as compris que $\log_b (x)= \dfrac{\ln(x)}{\ln(b)}$ le reste vient tout seul.

Tu as donc $\log_5 \left(\dfrac{1-x}{x-5}\right) = \dfrac{1}{\ln(5)}\ln \left(\dfrac{1-x}{x-5}\right)$

Il te faut donc que (1-x)(x-5) > 0 ce qui te donne (x < 1 et x > 5) ou (x > 1 et x < 5) et évidemment seule la seconde solution est envisageable.

Donc, dans tout ce qui suit, x est supposé remplir la condition en gras.

Les limites sont clairement faciles à déterminer puisqu'on peut écrire $f(x) = \dfrac{1}{\ln(5)} (\ln(x-1) - \ln(5-x))$ et dans les deux cas, l'opérande tend vers 0+ et c'est le signe qui est devant qui donne la direction à suivre.

f est clairement continue et dérivable sur son domaine de définition et l'étude en 1 (resp. 5) est équivalente à l'étude de $\ln(x-1)$ resp $( \ln(5-x)$ )

$f'(x) = \dfrac{1}{\ln(5)} \left(\dfrac{1}{x-1} - \dfrac{1}{5-x}\right) > 0$ et on déduit que f est croissante.

$f(x)\geq 1 \Leftrightarrow \dfrac{1}{\ln(5)}\ln \left(\dfrac{1-x}{x-5}\right) \geq 1 \Leftrightarrow \ln \left(\dfrac{1-x}{x-5}\right) \geq \ln(5)$ et tu finis.

La bijectivité de f : tu joues sur le fait que f' existe en tout point est est > 0

Quant à $f^{-1}$ je ne fais pas l'injure de te mettre sur la piste.

Posté par re : Fonction logarithme 19-01-17 à 22:03

J'ai oublié un petit détail : $\ln(5) > 0$ ... ça peut toujours servir ...

Posté par re : Fonction logarithme 19-01-17 à 22:19

jsvdb @ 19-01-2017 à 22:02

Bonjour CloudNine

Une fois que as compris que $\log_b (x)= \dfrac{\ln(x)}{\ln(b)}$ le reste vient tout seul.

Tu as donc $\log_5 \left(\dfrac{1-x}{x-5}\right) = \dfrac{1}{\ln(5)}\ln \left(\dfrac{1-x}{x-5}\right)$

Il te faut donc que (1-x)(x-5) > 0 ce qui te donne (x < 1 et x > 5) ou (x > 1 et x < 5) et évidemment seule la seconde solution est envisageable.

Donc, dans tout ce qui suit, x est supposé remplir la condition en gras.

Les limites sont clairement faciles à déterminer puisqu'on peut écrire $f(x) = \dfrac{1}{\ln(5)} (\ln(x-1) - \ln(5-x))$ et dans les deux cas, l'opérande tend vers 0+ et c'est le signe qui est devant qui donne la direction à suivre.

f est clairement continue et dérivable sur son domaine de définition et l'étude en 1 (resp. 5) est équivalente à l'étude de $\ln(x-1)$ resp $( \ln(5-x)$ )

$f'(x) = \dfrac{1}{\ln(5)} \left(\dfrac{1}{x-1} - \dfrac{1}{5-x}\right) > 0$ et on déduit que f est croissante.

$f(x)\geq 1 \Leftrightarrow \dfrac{1}{\ln(5)}\ln \left(\dfrac{1-x}{x-5}\right) \geq 1 \Leftrightarrow \ln \left(\dfrac{1-x}{x-5}\right) \geq \ln(5)$ et tu finis.

La bijectivité de f : tu joues sur le fait que f' existe en tout point est est > 0

Quant à $f^{-1}$ je ne fais pas l'injure de te mettre sur la piste.

Merci pour votre aide,

'' f est clairement continue et dérivable sur son domaine de définition et l'étude en 1 (resp. 5) est équivalente à l'étude de \ln(x-1) resp ( \ln(5-x)) '': Je n'ai pas compris.
Pour étudier la dérivabilité sur son domaine de définition.
Il faut que $\lim_{x->1+} \frac{f(x) - f(x_0)}{x - x_0} = \lim_{x->1-} \frac{f(x) - f(x_0)}{x - x_0}$ = f(1). Le seul problème ici, je suis bloqué car ln(0) n'existe pas.

Posté par re : Fonction logarithme 19-01-17 à 22:38

Pour

jsvdb @ 19-01-2017 à 22:02

Bonjour CloudNine

$f(x)\geq 1 \Leftrightarrow \dfrac{1}{\ln(5)}\ln \left(\dfrac{1-x}{x-5}\right) \geq 1 \Leftrightarrow \ln \left(\dfrac{1-x}{x-5}\right) \geq \ln(5)$ et tu finis.

Si j'ai bien compris, en appliquant l'exponentielle sur ln.
Je trouve x≤ 13/3

Posté par re : Fonction logarithme 19-01-17 à 22:40

N.B. : tu n'es pas obligé de citer l'entièreté du message à chaque fois ...

Lorsque tu vas étudier ta fonction en 1+, tu vois bien que le terme $\ln(5-x)$ reste borné devant $\ln(1-x)$ qui explose, donc, en 1, on a juste besoin de se contenter de regarder $\ln(1-x)$

Sinon, étudier la limite du taux d'accroissement de f en 1+ consiste simplement regarder la limite de la dérivée en 1+ et certainement pas de le calculer puisque f(1) n'existe pas !

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

analyse en post-bac
21 fiches de mathématiques sur "analyse" en post-bac disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Fonction logarithme

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths