Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... LicenceMaths 2e/3e a AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau LicenceMaths 2e/3e a
Partager :

Fonction non continue

Posté par Profil Shipz 04-08-23 à 15:44

Bonjour,

Dans un exercice de mon cours, on considère l'espace vectoriel E des fonctions continues de [0;1] à valeurs réelles, muni de la norme 1 définie par \|f\|_1=\int_0^1 |f(t)|dt.

On considère alors l'application linéaire u définie sur E (et à valeurs réelles) par u(f)=f(\frac{1}{2}).

Il me semble que u n'est pas continue pour la norme 1.
Si c'était le  cas, il existerait une constante positive non nulle telle que pour tout élément f de E, |u(f)|\le C\|f\|_1, autrement dit |f(\frac{1}{2})|\le C \int_0^1 |f(t)|dt.

Le problème, c'est que je n'arrive pas à construire une fonction (ou une suite de fonctions) permettant d'aboutir à une contradiction.
J'ai essayé avec f_n(t)=ne^{-nt}, avec f_n(t)=t^n ou encore avec une fonction triangle, mais pas de contradiction en vue.

Après, peut-être que mon intuition est fausse et que u est continue pour la norme 1.

Auriez-vous une piste ?

Merci !

Posté par
Rintarore : Fonction non continue 04-08-23 à 17:09

Bonjour,

si on peut construire une suite de fonctions vérifiant

\forall n \geq 1 ~:~ \int_0^1 |f_n(t)| dt = \dfrac{|f(1/2)|}{n}

alors c'est gagné, tu vois pourquoi ? J'affirme qu'une telle suite existe, réussirais-tu à en exhiber une ?

Posté par
Ulmierere : Fonction non continue 04-08-23 à 17:11

Le site rame aujourd'hui...

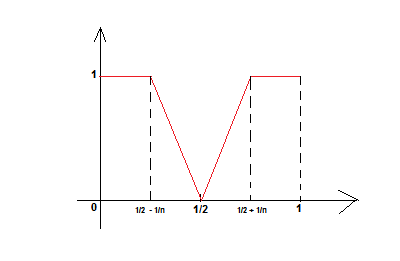
Regarde ce qui se passe avec la fonction affine par morceaux qui est nulle sur [0,1/2-\delta_n] et sur [1/2+\delta_n, 1] et en forme de pic atteint en 1/2 où elle prend la valeur 1.
C'est une fonction continue positive sur [0,1] dont la norme L1 est l'aire du triangle, qui est 2\delta_n.
Si u est continue, alors pour chacune de ces fonctions on aura 1 \leqslant 2C\delta_n, ce qui mène à une contradiction si tu fais tendre la suite \delta vers 0 alors que C>0

Posté par
carpediemre : Fonction non continue 04-08-23 à 17:13

salut

quand on n'arrive pas à trouver de contre-exemple alors peut-être est-ce vrai ou du moins on se dit qu'on va montrer que c'est vrai ... jusqu'à que ça devienne faux si tel est le cas (ie on se trouve à une étape qui ne permette plus d'avancer ou qui aboutit à une contradiction)

Shipz @ 04-08-2023 à 15:44

Dans un exercice de mon cours, on considère ...
On considère alors ...
Il me semble que u n'est pas continue pour la norme 1

et si tu nous donnais l'énoncé exact ?

Posté par
carpediemre : Fonction non continue 04-08-23 à 17:26

Ulmiere @ 04-08-2023 à 17:11

Le site rame aujourd'hui...

ouais c'est pourquoi j'ai posté une première fois et voulais poursuivre sur la même idée que tu as proposée ...

en proposant la fonction f_n(x) = 4^n [x(1 - x)]^n

Posté par Profil Shipzre : Fonction non continue 04-08-23 à 20:29

Bonsoir,

C'est l'énoncé exact.
Merci beaucoup pour vos réponses pédagogiques !
Je retiendrai ces méthodes. J'avais l'intuition, mais je n'ai pas encore les automatismes dans ce genre de situation.

A bientôt

Posté par Profil Shipzre : Fonction non continue 04-08-23 à 20:29

Carpediem, qu'est-ce qui t'as fait penser à cette fonction ?

Posté par
Rintarore : Fonction non continue 05-08-23 à 13:01

Bonjour,

je donne ma solution puisque tu as compris à l'aide des autres réponses. Je pensais à la suite de fonctions toute bête

f_n(x) = \dfrac{2x}{n}

Tu as eu une bonne intuition, la valeur en un point précis d'une application peut être "relativement" plus grande que l'intégrale de cette même fonction. L'exemple de Ulmière reflète bien ça.

Posté par
carpediemre : Fonction non continue 05-08-23 à 13:19

Shipz @ 04-08-2023 à 20:29

Carpediem, qu'est-ce qui t'as fait penser à cette fonction ?
parce que je pensais au même type de fonction que Ulmiere : une sorte de fonction chapeau
(un grand classique) en plus que continue que la sienne puisque la mienne est dérivable et même C

mais son intégrale est plus difficile à calculer ...

Posté par
verdurinre : Fonction non continue 05-08-23 à 19:42

Salut carpediem.
On peut démontrer que :
\begin{aligned}\nolimits\int_ 0^1x^n(1-x)^n\text{d}x=\frac{(n!)^2}{(2n+1)!}\end{aligned}

Posté par
Ulmierere : Fonction non continue 05-08-23 à 20:19

Dans ce cas, \dfrac{(n!)^2}{(2n+1)} \sim \dfrac{\sqrt{2\pi}}{2n+1} \cdot\dfrac{ne^{-2n}n^{2n}}{\sqrt{2}n^{1/2}e^{-2n}2^{2n}n^{2n}} \sim \dfrac{\sqrt{n\pi}}{4^n(2n+1)} et l'intégrale que nous cherchons est équivalente à \dfrac12\sqrt{\dfrac{\pi}{n}} donc tend vers 0. C'est un poil plus compliqué avec la formule de Stirling/fonction Beta incomplète qu'avec les petits chapeaux qui approximent \delta_{1/2}

Posté par
carpediemre : Fonction non continue 06-08-23 à 13:33

ouais !!

je voulais une fonction avec une formule "unique" mais ça complique la suite ...

Posté par
elhor_abdelali Correcteurre : Fonction non continue 06-08-23 à 16:02

Bonjour

On peut aussi pour étabir la non continuité de la forme linéaire u

montrer que son noyau \mathcal H (qui est un hyperplan de E) n'est pas fermé.

En effet en considérant (par exemple) la suite (\varphi_n)_{n\geqslant2} d'éléments de \mathcal H

définie par \Large\boxed{\varphi_n(x)=\left\lbrace\begin{array}l n|x-\frac{1}{2}|~~si~~|x-\frac{1}{2}|\leqslant\frac{1}{n}\\\\1~~~~~~~~~~~sinon\end{array}\right.}

on établit assez facilement que la suite (\varphi_n)_{n\geqslant2} converge pour la norme ||.||_1 vers la fonction constante 1\notin\mathcal H.


Remarque : on peut même établir la densité de \mathcal H dans \left(E,||.||_1\right)

en montrant que pour tout f\in E on a \Large\boxed{\lim_n||f-f\varphi_n||_1=0} sauf erreur de ma part bien entendu

Fonction non continue

Posté par Profil Shipzre : Fonction non continue 07-08-23 à 07:15

Merci à tous et toutes pour vos réponses éclairées !!


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !