Inscription / Connexion Nouveau Sujet
fonction racine carrée
bonjour
la fonction racine carrée est la fonction f définie sur intervalle 0; +l'infinie par f(x)=racine carré de x
1) tracer a l'aide de la calculatrice la représentation graphique de cette fonction ds un repère orthonormé d'unité 1cm
etablir un tableau de variation de f a l'aide du graphique
etudions le sens de variation de f sur interalle 0; +l'infinie
soient a et b deux réels tels que 0 a plus petit que b
a plus petit que b
démontrer que racine caré de b - racine carré de a= b-a sur racine caré de b + racine carré de a
merci de votre aide!
non je ne sais pas comment on fait et mon prof ne ma pas expliquer car il ne connait pas la marque de ma calculette pouriz vous m'aider svp?
sa yé j'ai ma fonction pouriez vous m'aider pour la question
etudions le sens de variation de f sur interalle 0; +l'infinie
soient a et b deux réels tels que 0a plus petit que b
démontrer que racine caré de b - racine carré de a= b-a sur racine caré de b + racine carré de a
la fnction ds un repére d'unité 5cm et je trouve sa
est ce que c'est sa??
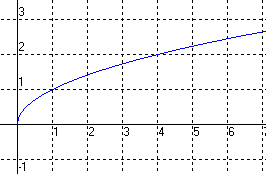
j'ai pri un modéle sur internet c'est la meme chose!
On te demande graphiquement le sens de variation. C'est juste dire en regardant la courbe "croissante" ou "décroissante"
Tu ne l'as pas faite sur ta calculatrice ? C'est dommage, ça t'aurait permis d'apprendre à le faire. Je m'en doutais un peu, d'ailleurs...
sur la casio tu vas dans graph, exe, tu tapes Y1=X^(1/2)
puis exe et draw et tu as ta courbe.
aa bas c'est sa le probléme je ne trouve jamais c'est quoi y!
Oui, elle est croissante. Essaie de faire la courbe sur ta calculatrice, comme ça tu sauras t'en servir. Si tu attends que les profs t'apprennent, tu pourras attendre longtemps...
Y1= est déjà écrit dans le menu de la calculatrice
toi tu tapes juste X^(1/2) ce qui veut dire racine de X
la touche X est sous la touche rouge sur la mienne. A gauche de la touche log
peu tu m'aider pour la suite??
etudions le sens de variation de f sur interalle 0; +l'infinie
soient a et b deux réels tels que 0a plus petit que b
démontrer que racine caré de b - racine carré de a= b-a sur racine caré de b + racine carré de a
bonsoir , petit probléme avec cet exo pouriez vous m'aider svp
la fonction racine carrée est la fonction f définie sur intervalle 0; +l'infinie par f(x)=racine carré de x
1) tracer a l'aide de la calculatrice la représentation graphique de cette fonction ds un repère orthonormé d'unité 1cm
etablir un tableau de variation de f a l'aide du graphique
(jusque la j'ai fait)
etudions le sens de variation de f sur interalle 0; +l'infinie
soient a et b deux réels tels que 0a plus petit que b
démontrer que racine caré de b - racine carré de a= b-a
sur racine caré de b + racine carré de a
Que peut on en déduire pour le signe de racine carré de b- racine carré de a?
merci de votre aide
*** message déplacé ***
j'ai fait jusqu'au tableau de variation de f al'aide du graphique!
*** message déplacé ***
ee non notre prof nous a jamais donné ce genre d'exo!
*** message déplacé ***
pour le tableau de variation?? ba la courbe est croisante!
*** message déplacé ***
ee oui! mais je n'y arrive toujours pas!
*** message déplacé ***
comment fait on pour démontrer que
racine caré de b - racine carré de a= b-a
sur racine caré de b + racine carré de a
*** message déplacé ***
ee oué mé il faut simplifier? et pk c'est 1??
le sujet c'est racine caré de b - racine carré de a= b-a
sur racine caré de b + racine carré de a
*** message déplacé ***
tu développes en haut avec une identité remarquable et tu as fini la question 1.
J'ai mis un 1 pour partir d'une fraction, c'est tout.
Je suis en seconde aussi (et dans le même chapitre que toi !)
*** message déplacé ***
sa yé j'ai trouvé! je pense ke c'est
racine carré de b- racine caré de a= racine caré de b²- racine carré de a ² sur racine carré de b + racine caré de A
mais que peut on déduire pour le signe de racine carré de b-racine carré de a?
*** message déplacé ***
Je te le poste au propre :
Maintenant, étudies le signe de ça :
(Comme hier...) et tu pourras finir la question.
*** message déplacé ***
le signe est positif!
quel propriété de la fonction racine caré vient-on de démontrer?
*** message déplacé ***
Oui, c'est bien positif !
Que peux tu en déduire pour comparer f(a) et f(b) (ou  a et
a et  b ) ?
b ) ?
*** message déplacé ***
Si la différence f(b)-f(a) est positive, alors f(b)>f(a).
(je te l'ai dit hier  )
)
donc f(b) > f(a)
et on sait que b > a.
Donc, quel est le sens de variation de la fonction sur cet intervalle ?
*** message déplacé ***


 [ ?
[ ?

