La définition de Arccos(y) pourrait être "l'unique x de tel que cos(x)=y"

Il résulte directement de la définition que cos(Arccos(y))=y sur le domaine de définition de Arccos qui est [-1,1].

Il résulte égalament de cette définition que Arccos(cos(x)) n'est pas, en général, égal à x puisque cos(x) est défini sur et que Arccos(y) appartient à .

On peut également dire que, x étant un réel donné, est le même nombre quel que soit , et que par conséquent ne peut être égal qu'à un seul nombre parmi l'infinité de réels avec

oui bien sûr, je voulais dire sur ....
merci de ta réponse... c'est pas mon jour aujourd'hui
A+

Salut tout le monde,

la fonction arccos est définie sur [-1;+1] et prend des valeurs dans [0;] car elle est la réciproque de la fonction "restreinte" de cos à [0;].

Pourquoi avoir "restreint" cos à [0;] ? ... tout simplement pour avoir une fonction continue et croissante afin d'employer le th de la bijection... Ce choix a donc été très arbitraire

ainsi, pour x [2;3], arcos(cos(x)) = x - 2
mais pour x [;2], arcos(cos(x)) = 2 - x  car cos(x) = cos (-x) = cos (2-x)

à urgo ..
tu as, d'autre part, fait une erreur dans ton post du 19/04 à 14h25  (désolé, je ne sais pas récupérer les citations)

En effet, si cos(2t) 0, alors 2t [-/2;+/2]  est faux !!!

c'est 2t + k.2  qui [-/2;+/2]  donc 2t [-/2 + k.2;/2 + k.2]
et ça change le résultat car t [-/4 + k.;/4 + k.]


J'ai pu voir que tu parlais de /., donc tu connais les classes d'équivalences.
Ton égalité est 2x = /2 , en classe, dans /2.
Ta division par 2 change la donne et te renvoies à /.

merci GGenn pour ta réponse très complète c'est très clair

de rien ....

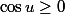
Salut!
Une remarque R/pi.R, c'est 0.
Je pense que vous vouliez parler de R/piZ, qui n'est pas un corps au passage.

j'ai beaucoup oublié sur ces notions ... mon intention était simplement d'expliquer à urgo le travail modulo 2.pi