Bonjour , ça existe aussi ....

1) deux maniére de procéder :
-On part de l'expression dévelloppée puis on factorise en passant par la forme canonique
-on part des expressions données puis on dévelloppe en esperant retomber sur f(x)

La premiére est plus élégante et "impressionante" je dirai et la 2éme est plus rapide ... De plus je ne crois pas que la premiére soit réellement acquise en 2nd ( bien qu'une fois qu'elle est comprise elle est facilement exploitable) donc je vais me contenter de la deuxiéme :








2)Calculer l'image de par f revient à calculer

Pour cela nous allons utiliser la premiere forme ( on aurait pu trés bien utiliser les autres mais celle-ci fait directement apparaitre un carré ce qui peut nous aider pour faire disparaitre la racine )






3) calculer le(s) antécédent(s) par f d'un nombre a revient à trouver les abscisse x vérifiant f(x)=a , c'est a dire résoudre l'équation f(x)=a

a)
<=>
<=>
<=>

Or , le produit ab est nul si et seulement si a ou b est nul .

donc si et seulement si x=0 ou x=-1

Les antécédents de 2 par f sont donc 0 et -1

b)c) Je te laisse les faire en raisonnant de la même façon

4)Pour nous occuper du signe du trinôme f , nous allons prendre la meilleur forme : (1-x)(x+2) . cette forme est trés utile car elle est entiérement factorisée donc facilement étudiable

- est strictement positif si x<1 , s'annule en 1 , et est négatif si x>1
- est positif si x>-2 , s'annule en -2 et est négatif pour x<-2

on en déduit le tableau de signe :


5) la calculatrice va nous donner . Pour le vérifier par le calcul , prenons notre chére forme canonique :

On sait que pour tout X réel , , donc pour tout x ,

d'où

et donc :

Ou encore

Ce dernier résultat montre alors que est le maximum de f

6)si tu te débrouilles bien tu devrais trouver quelque chose comme ça :



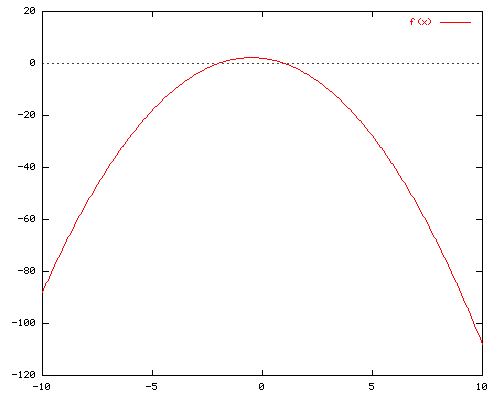
Voila , bon courage pour le peu qu'il te reste à faire de cet exercice