Inscription / Connexion Nouveau Sujet
fonctions
Bonsoir , yaurait-il quelqu'un qui pourrait me donner un coup de pouce pour résoudre cet exercice svp.
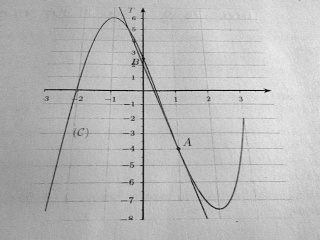
La fonction F dont la courbe (C) est définie sur l'intervalle [-2.5;3] par f(x)=x3-1.5x²-6x+2.5
1.Calculer f(-1)
2.a. Calculer f'(x)
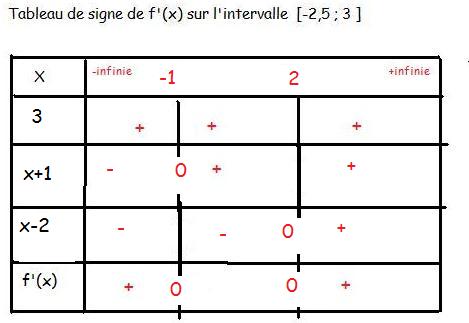
b. Vérifier que f'(x)=3(x+1)(x-2)
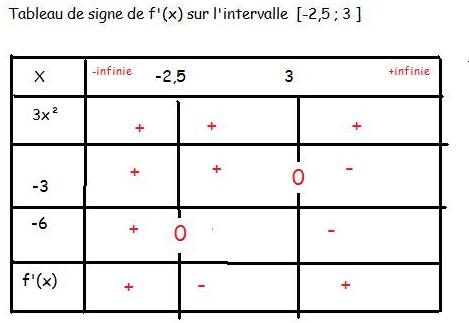
c. Etudier le signe de f'(x) sur l'intervalme [-2.5;3] à l'aide d'un tableau de signe
3. En déduire le tableau de variation complet de la fonction f sur l'intervalle [-2.5;3]
Bonsoir, f(-1), il suffit que tu remplace x par -1. dérivation c'est simplement dériver un polynôme. Tu ne sais pas ?
non f(-1)=6 (tu aurais pu regarder la figure pour vérifier ce que tu avais trouvé)
Étrange que l'on te donne un exercice où il faut dériver si tu n'as pas appris.
la dérivée de kxn est knxn-1 (et la dérivée d'une constante est nulle) donc tu dérives chaque terme et tu ajoutes les dérivées.
Ici ça te donne f'(x)=3x²-3x-6
j'ai réessayer plein de fois et je trouve -6 .. pouvez vous me détailler votre calcul svp .
pouvez vous m'expliquer en détail la dérivé svp
montre plutôt tes calculs, je te dirais où ça ne va pas.
je t'ai donné la formule pour la dérivée par exemple si tu dérives x3 c'est de la forme xn, la dérivé est nxn-1, tu appliques cette formule et ça fait 3x2, ça n'est pas très compliqué.
f(-1)=(-1)3-1.5*(-1)² -6*(-1) +2.5
= -1-1.5-6+2.5
= -6
pour la dérivée de f'(x) je trouve
x3-1.5x²-6x+2.5
= 3x²-1.5*2x-6
= 3x²+6.5-6
= 3x²+0.5
Ah oui c'est juste une erreur de signe !
donc pour la dérivée :
= 3x²-1.5x²*2x-6
= 3x²-3x-6
et apres je ne peut plus réduire donc la solution finale est 3x²-3x-6
vérifier f(x) ? c'est une des questions ça ? tu veux dire vérifier que le graphe est conforme ?
vérifie déjà que les extremums locaux sont bien ceux que tu vois sur le graphe, que A(1;-4) est sur la courbe, que la tangente en A est conforme à ce que tu vois, etc...
oui c'est une des questions :
2.a. Calculer f'(x)
b. Vérifier que f'(x)=3(x+1)(x-2)
c. Etudier le signe de f'(x) sur l'intervalme [-2.5;3] à l'aide d'un tableau de signe
3. En déduire le tableau de variation complet de la fonction f sur l'intervalle [-2.5;3]
je ne sais pas c'est quoi des extremums locaux
ha vérifier que f'(x)=3(x+1)(x-2) ! rien à voir
Donc là il te suffit de développer 3(x+1)(x-2) et vérifier que tu retombes bien sur 3x²-3x-6
c'est juste un moyen rapide de te faire trouver les valeurs qui annulent la dérivée.
a d'accord merci et pr le tableau de variation c'est l'intervalle qui me bloque je doit m'en occuper ?
 tu ne sais pas faire le produit de deux facteurs ? ça n'est pas un + entre (x+1) et (x-2) c'est un multiplié !!
tu ne sais pas faire le produit de deux facteurs ? ça n'est pas un + entre (x+1) et (x-2) c'est un multiplié !!
ben non si tu multiplies (x+1)(x+2) par exemple ça donne x²+2x+x+2 ,toi tu n'as même pas x² (et ils réapparaissent à la fin d'ailleurs. N'importe quoi).
ahh d'accord moi je n'est pas appris comme sa c'est pour sa ..
j'ai fai la question 3 pour le tableau de variation de la fonction f pouvez vous me dire si c'est bon svp
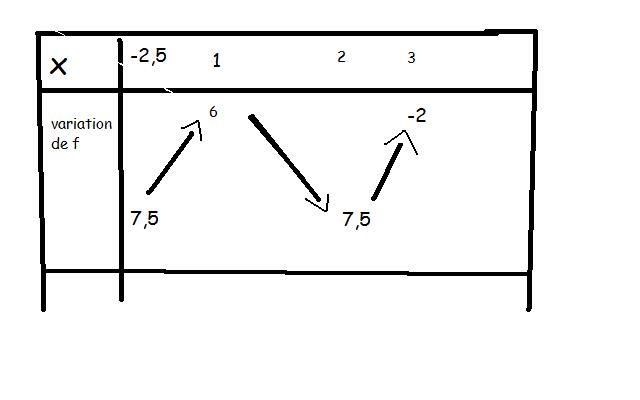
pour x=-1 le premier maximum et pas x=1 mais sinon c'est bon. D'habitude on met aussi une ligne avec f'(x) et son signe.
non ça je ne comprends pas. f'(x)=3(x+1)(x-2) donc la fonction s'annule pour -1 et 2 et est positive à l'extérieur de ces racines et négative entre. Et en plus au 3c on te demande le tableau de variation de la fonction f, pas de f'.
Et puis pour avoir le signe de f'(x)=3x²-3x-6, on factorise, on n'ajoute pas les signes de chaque terme. la somme d'un + et d'un - ne fait pas forcement - !! tu confonds tout, là.
je me suis tromper c'est le 2.c ou on me demande le signe de f'(x) sur l'intervalle [-2,5;3]
je ne comprend pas , expliquez moi svp
f'(x)=3x²-3x-6=3(x+1)(x-2) on veut le signe d'un polynôme du second degré.
tu peux faire un tableau de signes en mettant une ligne avec x+1, une ligne avec x-2 et en étudiant le signe du produit.
Ou bien tu sais par coeur (ce qui est très utile) qu'un polynôme du second degré est du signe de son terme de plus haut degré à l'extérieur de ses racines quand il en a. et tu peux répondre immédiatement quand est-ce que c'est positif ou négatif.
oui c'est bien. (au lieu de - et +
et + , tu devrais mettre -2,5 et 3 puisque l'on te demande d'étudier dans cet intervalle. et entre -1 et 2 met un -)
, tu devrais mettre -2,5 et 3 puisque l'on te demande d'étudier dans cet intervalle. et entre -1 et 2 met un -)