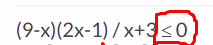Bonjour,
Ce sont les tableaux de 12h17 qui sont corrects, donc à utiliser.

Pour 1), on cherche quand le quotient est positif ou nul ; tu regardes donc quelles sont la ou les colonnes où il y a des + dans la dernière ligne.

Commence par traiter 1) en traduisant avec un ou plusieurs intervalles.

Je vais essayer de mettre en image ce que Sylvieg a mis en Français

ton inéquation à résoudre est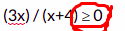


la lecture de ce signe veut dire que tu veux que le quotient soit positif ou nul
Positif dans un tableau c'est quand tu mets un +
nul dans le tableau c'est quand tu mets un 0

donc à la dernière ligne (car c'est là qu'est écrit le quotient) de ton tableau tu dois repérer partout où il y a soit un + soit un 0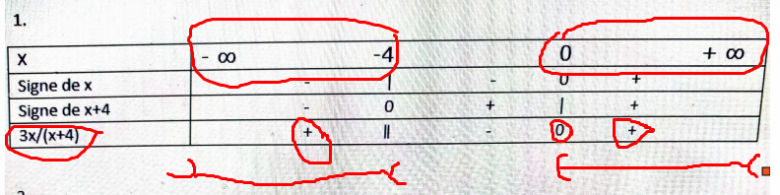



et donc cela fait, tu vas lire tout en haut les x qui répondent à ces valeurs
en faiasnat attention si les bornes sont ouvertes ou fermées
et je lis
x ]-, -4[[0 ; + [

ici il y a deux intervalles qui répondent à la question et je les réunis donc avec le signe qui indique une union

on attend que tu fasses exactement la même démarche pour le tableau 2

x ∈]- ∞ ; -3 [ ∪ [1/2 ; 9 ; +∞[

on veut que (9-x)(2x-1) / x+3 ≤ 0

donc ta réponse est fausse

(9-x)(2x-1) / x+3 ≤ 0
x ∈]- ∞ ; -3 ] ∪ ]1/2 ; 9 ; +∞[

Bonjour

Négatif  s'écrit aussi
Positif s'écrit aussi

Je corrige pour lever toute ambiguïté

Négatif  s'écrit aussi
Positif s'écrit aussi

Merci hekla
avec les erreurs de frappe  difficile à se concentrer, réfléchir et se relire ...

Vous auriez pu donner la solution de cette inéquation

x ∈]- ∞ ; -3 ] ∪ ]1/2 ; 9 [

oui ce que je viens de faire et nos messages se sont croisés

Quel signe voyez-vous entre et ?  et  le signe de l'expression doit être  négatif ou positif ?

le signe +

Vous donnez toujours la même réponse malgré l'erreur signalée.

et on veut  ?

ça veut dire quoi ça, ce que j'ai entouré en rouge ?

pas compris

négatif

oui, négatif
et quel est le signe dans le tableau qui va dire que c'est négatif ? + ou - ?

signe -

eh bien, tu es quand même capable de lire les endroits du tableau où dans la dernière ligne il y a le signe moins

eh bien oui vu que maintenant c'est bien expliqué
donc, je lis sur le tableau :
x ∈] -3 ; 1/2 et 9 ; +∞[

Il manque deux crochets

il manque des crochets

d'accord,
x ∈]-3 ; 1/2 ] ∪ ] 9 ; +∞ [

non

exagères ? eh non car je les déjà dit lorsque je ne comprends pas et c'est pas mal d'expliquer étape par étape si besoin et c'est mon cas car faut dire il y a des erreurs de frappe où ça m'embrouille

le faux c'est ça : ∪ ?

non, un crochet mal mis

ce matin à 9h29 je n'ai pas dit le contraire et même je rajoute à 10h48 le tableau est bien fait avec la correction où ils étaient mes erreurs et la j'ai compris donc tout simplement j'ai juste souligné la précision du faux pour pas me perdre.
Exemple le non à 18h38 ? c'est bien de préciser l'erreur ? car un simple non pour moi c'est faux et c'est à revoir.

Ok pour le crochet : x ∈[-3 ; 1/2 ] ∪ ] 9 ; +∞ [ ?

En la fraction n'est pas définie  par conséquent on doit avoir un crochet ouvert ]-3

en 1/2 la fraction est définie et l'inégalité est large   donc 1/2 est une solution donc on le prend  pour cela le crochet est fermé

pour 9 idem

en c'est toujours ouvert  donc

Ensemble des solutions maintenant  

d'accord, merci hekla, je fais ça de suite

x ∈]-3 ; 1/2 ] ∪ 9 ] ; +∞ [

ah mince

@gabno,
Il y a un bouton "Aperçu" à côté du bouton "POSTER".
Pense à l'utiliser.

x ∈]-3 ; 1/2 ] ∪ 9 ] ; +∞ ]

d'accord sylvieg et merci pour l'info

ok malou

Vous pouviez en même temps donner votre réponse

n'oubliez pas aperçu avant de poster  et de lire ce que l'on vous a dit

x ∈]-3 ; 1/2 ] ∪ [ 9 ; +∞ [

Oui

merci,
est-ce que c'est bon si j'écris tout ça :
1. (3x) / (x+4) ≥ 0
     3x = 0 <=> x = 0 et est positif pour x > 0
     x + 4 = 0 <=> x = -4 donc x+4 est nul en x = -4 et est positif pour x > -4
On conclut :
x ∈]- ∞ ; -4 [ ∪ [0 ; +∞[

2. (9-x)(2x-1) / x+3 ≤ 0
      9-x = 0 <=> x = 9 donc 9 - x est nul en x = 9 et est positif pour x > +9
      2x-1 = 0 <=> 2x = 1 <=> x = 1/2 donc 2x-1 est nul pour x = 1/2 + et est positif pour x > 1/2
     x+3 = 0 <=> x = -3 donc x+3 est nul pour x=-3 et est positif pour x > -3
On conclut :
x ∈]-3 ; 1/2 ] ∪ [ 9 ; +∞ [

Il vaudrait mieux écrire

tableau de signe et conclusion

   manque des parenthèses

  idem pour les 2 autres

le tableau de 13 :40 et la conclusion de 20:17

1. (3x) / (x+4)
3x > 0 si x > 0
x + 4 > 0 <=> x > -4
On conclut :
x ∈]- ∞ ; -4 [ ∪ [0 ; +∞[

2. (9-x)(2x-1) / (x+3) ≤ 0
     9-x > 0 <=> x < 9
     2x-1 > 0 <=> x > 1/2
     x+3 > 0 <=>  x > -3
On conclut :
x ∈]-3 ; 1/2 ] ∪ [ 9 ; +∞ [

Là je trouve que c'est un peu rapide  ajoutez  le tableau de signes et  ce sera très bien

1. (3x) / (x+4)
3x > 0 si x > 0
x + 4 > 0 <=> x > -4
On conclut :
x ∈]- ∞ ; -4 [ ∪ [0 ; +∞[

Tableau :