salut

il ne faut pas résoudre des équations mais des inéquations !!



ainsi on sait où on doit mettre le signe + dans le tableau ...

Bonjour à vous deux
gabno, voilà une fiche que tu peux travailler cinq exercices utilisant les tableaux de signes

Juste une question !!!
le signe ≥ (ne sont du même sens pour toutes les inéquations?)

3x ≥ 0 ⟺ 0
(x+4) ≥ 0 ⟺ -4
(9-x) ≥ 0 ⟺ 9
(2x-1) ≥ 0 ⟺ 1/2
x+3 ≥ 0 ⟺ -3

carpediem n'est plus là apparemment

tes équivalences n'ont pas de sens
vois cette fiche alors : Exercice Equations et inéquations

Pour moi si !!! ça m'embrouillerais car les signes sont mis comme ça dans l'exercice et c'est un pb si ça change, je ne veux pas être embrouillé (je me répète) !!! si vous choisissez  ≥  faite le savoir !!! je comprendrais et suivre par étape l'exercice !

malou j'ai vu ton exercice que tu m'as proposé de voir et j'ai compris quand tu as écrit "tes équivalences n'ont pas de sens" pourtant c'est ce que j'ai fait au début mais carpediem m'a écrit "il ne faut pas résoudre des équations mais des inéquations !!" donc j'ai suivi son exemple ...

Voilà et où sont les erreurs :
1. (3x) / (x+4) ≥ 0
3x = 0

x+4 = 0
x = -4
          
2. (9-x)(2x-1) / x+3 ≤ 0

9-x = 0 ⟺ 9

2x-1= 0
x = 1/2

x+3 = 0
x = -3

x+3 = 0
x= -3

Je corrige mon erreur : "9-x = 0 ⟺ 9"
9-x = 0
x=9

"Désolé je ne peux pas mettre de tableau "

Tableau :

x   -∞                    -4           -3                   0                 1/2    9               +∞

3x                                                                               -    0     +
x+4                         +        0      -
9-x                                                                                                                                 0
2x-1                                                                                               -        0        +
x+3                                                      +    0     -

alors :
dans la 2e fiche que je t'ai fléchée, on dirait :
3x=0 pour x=0
puis
3x > 0 revient à x > 0
ce qui veut dire en Français, que 3x est positif lorsque x est positif
ce qui veut dire dans le tableau
3x est positif c'est à dire je mettrais un + dans mon tableau
lorsque x est positif donc à droite de 0

mais tu dois faire un tableau différent pour chaque inéquation

fais tes tableaux sur ton papier, et prends une photo
et poste ton tableau en tant qu'image

d'accord merci malou, je vais aller en cours là et je reprend où nous étions après.
A tout à l'heure.

juste avant je voulais savoir lorsque tu m'écris "3x est positif c'est à dire je mettrais un + dans mon tableau lorsque x est positif donc à droite de 0 " => C'est ce que j'ai mit à droite du 0 un + ? Ou j'ai mal compris ?

oui, mais tout est décalé
donc on ne peut pas lire vraiment
tu feras sur ton papier et tu prendras en photo

3x = 0 <=> x = 0    ok

mais la nullité ne donne pas le signe !!!

sais-tu maintenant quand 3x est positif ? négatif ?

je choisis pour déterminer le signe de chaque facteur

je ne comprend plus à rien !!!
2 versions différentes !!!
je parle des signes : ≥ ou  ≤  car pour le 1 et le 2 sont différents!!!
Une fois ça ok =>3x = 0 <=> x = 0    une fois non car tes équivalences n'ont pas de sens!!!
je dois comprendre quoi au final !!! En faite je voulais juste savoir si ces signes ≥ ou  ≤  changent quelque chose au calcul ou tout simplement mettre les signe = pour les équations nuls, bref

J'ai fait ça , est-ce que c'est bon ?
3x = 0 <=> x = 0
(x+4)= -4 ⟺ x = -4
(9-x) = 9 ⟺ x = 9
(2x-1) = 0 ⟺ x = 1/2
x+3 = 0 ⟺ x = -3

après j'ai juste besoin de comprendre au niveau du tableau, si je peux avoir un exemple comme 3x = 0 <=> x = 0

je me corrige :
3x = 0 <=> x = 0
(x+4)= -4 ⟺ x = -4
(9-x) = 9 ⟺ x = 9
(2x-1) = 1/2 ⟺ x = 1/2
x+3 = -3 ⟺ x = -3

peux-tu te relire avant de poster ?
car là tu n'as rien rectifié...

et nous lire attentivement pour comprendre ce qu'on te dit ...

d'accord,
1. (3x) / (x+4) ≥ 0
3x = 0 <=> x = 0 et est positif pour x >0
x+4 = 0 <=> x = -4 donc x+4 est nul en x=-4 et est positif pour x>-4

justement je lis 2 versions car chacun s'exprime à sa manière donc j'essai de vous comprendre...

c'est bon pour le 1 ?

super merci ! je continue je fais le 2

attention, pour le 1) il te restera le tableau à faire pour trouver le signe de ton quotient

2. (9-x)(2x-1) / x+3 ≤ 0

       9-x = 0 <=> x = 9 donc 9-x est nul en x=9 et est positif pour x>9

       2x-1 = 0 <=> 2x = 1 <=> x = 1/2 donc 2x-1 est nul pour x=1/2 et est positif pour x>1/2

       x+3 = 0 <=> x = -3 donc x+3 est nul pour x=-3 et est positif pour x>-3

et voila pourquoi je dis ce que je dis !!!

donc dans la ligne du signe de 9 - x je mets le signe + avant 9

donc dans la ligne du signe de 2x - 1 je mets le signe + après 1/2

...

non je parle pas du signe + !!! je parle de ces signes là => ≤ ou ≥ au niveau du calcul !!!
Alors si j'ai bien compris :
9-x = 0 <=> x = 9 donc 9-x est nul en x=9 et est positif pour x>+9
2x-1 = 0 <=> 2x = 1 <=> x = 1/2 donc 2x-1 est nul pour x=1/2 et est positif pour x>1/2+

1. Tableau

je vais faire maintenant le tableau pour le 2.

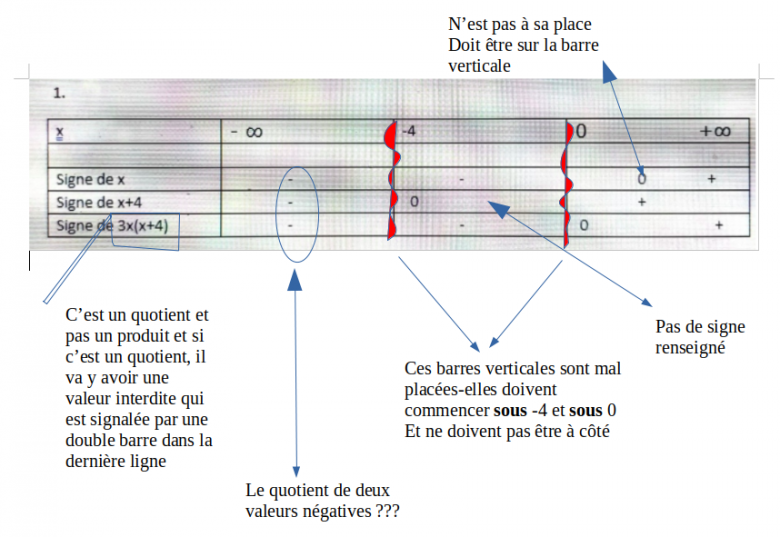
c'est plutôt un quotient pour la dernière ligne ... et n'oublie pas les valeurs interdites !!

et c'est quoi ces doubles signes dans une même case ?

revois les exercices et leur corrigé donnés dans le premier lien par malou

d'accord !!!
j'ai refait mais pas sur...

quelqu'un peux m'aider s'il vous plait , merci

Bonjour,
Pas le temps de répondre en détails.
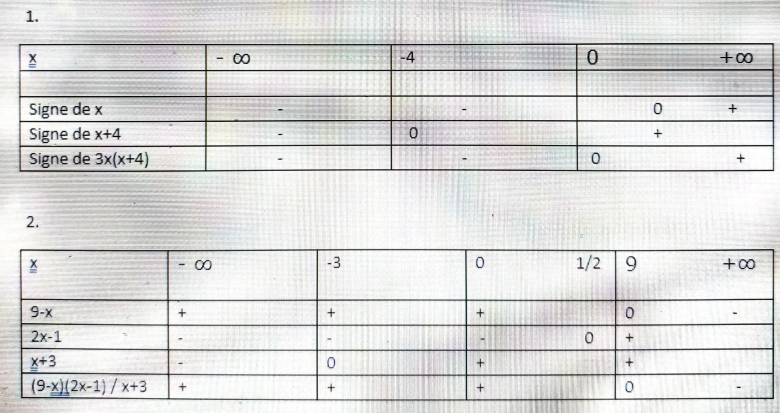
Dans tes tableaux, tu mets + systématiquement à gauche du zéro.
Ce n'est bon que lorsque le coefficient de x est négatif.
Comme dans 9-x.
Pour tous les autres, c'est - à gauche.

et puis les 0 dans les 2e, 3e, ...lignes doivent être positionnés juste en dessous de certaines valeurs et non pas dans les "cases"
je ne sais pas avec quoi tu fais ces tableaux
mais je crois qu'il vaudrait vraiment mieux que tu fasses ça avec règle, papier, crayon
parce que là on n'avance pas beaucoup

je t'ai donné des liens où tout est expliqué ligne par ligne
et toi tu grilles les étapes sans arrêt...donc tu as faux

bonjour,
d'accord merci

un tableau à la fois s'il te plaît, il y a trop à dire

pour les barres verticales , j'ai compris qu'il faut que je les met en dessous de -4 et 0. (donc sur ma feuille au propre je le ferai car là avec le tableau ce n'est pas possible) + est ce que c'est bien ça à la dernière ligne : [0;-4] ?

sinon l'autre tableau c'est bon ?

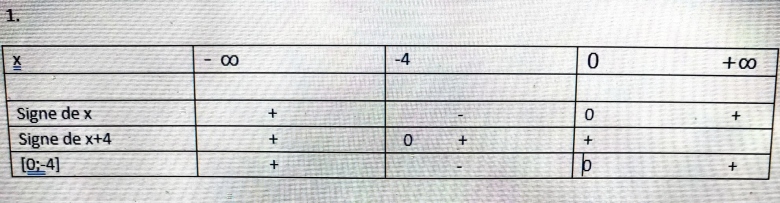
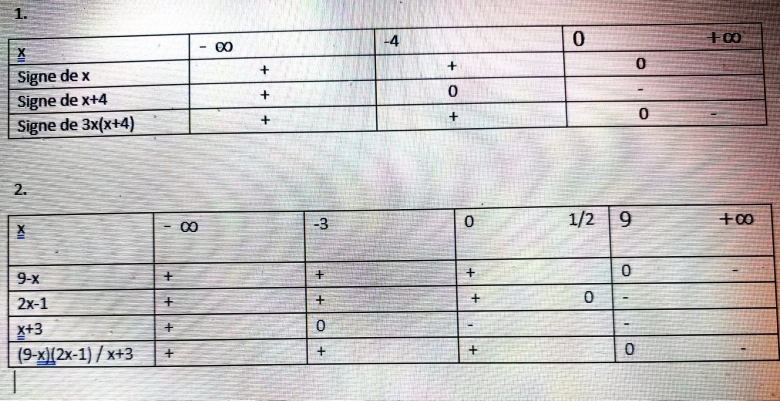
Aucun des tableaux n'est bon.
On a l'impression que tu ne cherches pas à comprendre comment les remplir.

Va voir les exercices 1 et 4 dans cinq exercices utilisant les tableaux de signes
Utilise le bouton "Voir la correction" tout en bas.

ah...
justement je suis ce qu'on me dit et j'essai de comprendre les raisons
Et là c'est beaucoup mieux ?

Tableau 1 :
Comment peux-tu mettre + pour x quand x est négatif ?

Tableau 2 :
Le réel 0 n'a aucune raison d'être présent dans la première ligne.
Le réel -3 y figure car -3 intervient pour le signe de x+3.
Le réel 1/2 y figure car 1/2 intervient pour le signe de 2x-1.
Le réel 9 y figure car 9 intervient pour le signe de 9-x.
Enlève ce 0 en haut. Il y aura une colonne de moins.
Les lignes sont correctes sauf la dernière, celle du quotient.

Les 2 tableaux :
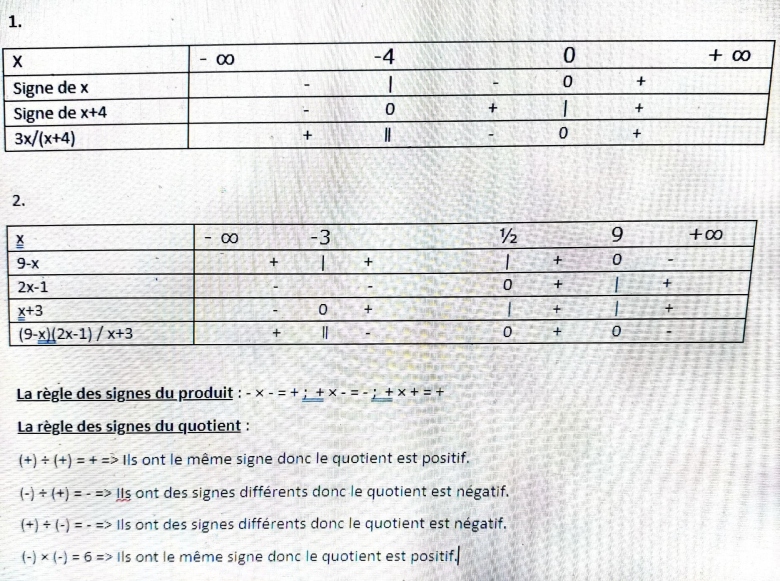
Tu as rempli la dernière ligne sans tenir compte de ce qui est au dessus.
Pour remplir la dernière ligne, on utilise la règle du signe d'un produit ou d'un quotient.

d'accord

oui!!!!!!!!!!!!!!!!!!!!!

il te reste à répondre à la question posée grâce à la dernière ligne de ton tableau à chaque fois

super!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
parcontre je suis pas sur pour la réponse à la question:
1.
3x > x+4
On conclut :
3x/(x+4) ≥ 0 pour x ∈]- 4 ; 0]

2.
(9-x)(2x-1) > x+3
On conclut :
(9-x)(2x-1) / x+3 ≤ 0 pour x ∈]- ∞ ; -3 [ ∪ [9 ; +∞[
ou ça ?
(9-x)(2x-1) / x+3 ≥ 0 pour x ∈]- 3 ; 1/2 ; 9]

On s'y perd un peu :

Citation :
3x/(x+4) 0 pour x ]- 4 ; 0]

" Non...
En bas de la colonne ]- 4 ; 0] du tableau de 12h17, c'est un - et pas un +. " ?

Oui, effectivement :
3x / (x+4)
3*(-3) / (-3+4)= -9
3*(-2) / (-2+4) =-3
3*(-1) / (-1+4) = -1

donc il te reste à répondre

je ne sais pas...