Inscription / Connexion Nouveau Sujet
Fonctions et dimensions d'un trapèze et d'un triangle
Bonjour 
Voilà, c'est l'un des exercices de mon dm, j'ai beau me creuser la tête, pas moyen d'avancer...
"ABCD est un trapèze rectangle et M un point du segment [AB].
On note x la longueur AM, f(x)) l'aire du triangle CMB et g(x) l'aire du trapèze AMCD.
Le graphiuque ci-dessous représente ces deux aires en fonction de x.
En vous aidant du graphique, retrouvez les dimensions du trapèze AMCD."
Le graphique donne juste deux courbes (on ne sait pas quelle courbe représente quelle fonction)
L'une est décroissante, telle que y : -2x + 14
La seconde est croissante, telle que y : 2x + 8
Elles se coupent en 11 pour x=1.5
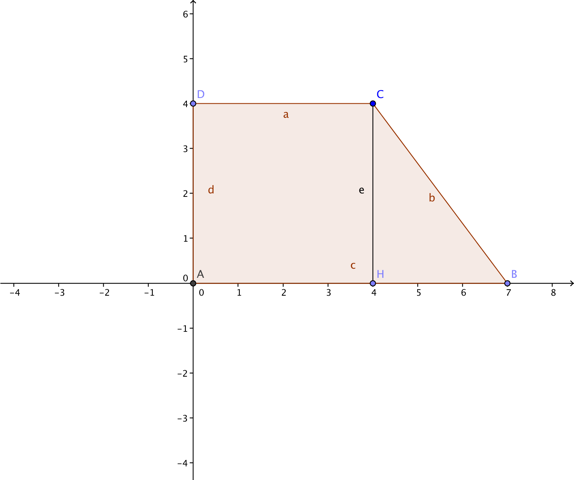
La figure nous donne un trapèze DCBA tel que (DC) et (AB) parallèles et M est point de (AB) tel que AM=x
La longueur MB étant donc égale à AB-x
(Désolée je n'ai pas pu scanner la figure, mais elle n'est pas à l'échelle ni quoi, c'est juste une figure d'indication de toutes manières)
Voilà, ce sont les seules indications données, aucune mesure n'est fournie.
Si quelqu'un pouvait m'aiguiller, ce serait vraiment génial...
Merci d'avance 
Dans le trapèze ABCD, (DC) parallèle à (AB)
et le trapèze est perpendiculaire en D et en A
(le triangle BCM est apparemment quelconque)
aire du trapèze AMCD
(x+DC)*DA/2
quand x croit aire croit donc la courbe d'équation y=2x+8 représente l'aire du trapèze
ensuite l'autre représente l'aire du triangle CMB
aire du triangle CMB
aire du trapèze ABCD - aire du trapèze AMCD=(AB+DC)DA/2-(x+DC)DA/2=DA/2(AB-x)
et la courbe y=-2x+14 représente cette fonction
je te laisse continuer
autres renseignements à exploiter le trapèze est rectangle
et les aires quand x=0 ou x=AB
Merci 
J'ai pas mal avancé, mais il reste un dernier petit point, je n'arrive pas à démontrer que AD=AC :/
quand x=0
g(x)=2x+8=> g(x)=8
g(x) = aire(AMCD)
8 = AD(DC+x)/2
sauf que je viens de m'embrouiller toute seule, à nouveau, je peux pas trouver AD et DC dans le même calcul, donc ni l'un ni l'autre...
Et du coup mon calcul pour trouver AB tombe à l'eau aussi
y=-2x+14 aire du triangle CMB
y=2x+8 aire du trapèze AMCD
aire totale =22 (en additionnant)
quand x=0
aire du triangle= aire du triangle CAB=14=AB*DA/2
aire du triangle ADC=8=AD*DC/2
AD*DC=16
AB*DA=28
DC/AB=16/28=4/7
quand x=AB
-2x+14=(AB-x)DA/2=0
-2x+14=0==>x=7=AB
DC=(4/7)AB=4
AD*DC=16==>AD=16/4=4
ensuite Pythagore pour CB
CB2=(7-4)2+42=25
Pour Pythagore, il faut bien prendre la hauteur de CMB (qui est donc égale à AD) pour avoir l'angle droit. J'appelle le pied de la hauteur Z, je me situe donc le triangle CZB, rectangle en Z.
CB²=CZ²+ZB²
or je n'ai pas ZB²
Dans ce que vous m'avez donné, CB²=(7-4)²+4²=25
je comprends, 7-4 = AB-x=MB
mais MB ZB
ZB
:/
Oui c'est cette figure là
mais je ne comprends pas comment on peut dire
AH=x=4
Parce qu'on ne connaît pas AB, on sait juste que MB=3 AM=4 AB=7