Bonjour!
Voici l'énoncé d'un devoir maison dont la dernière question me pose problème:
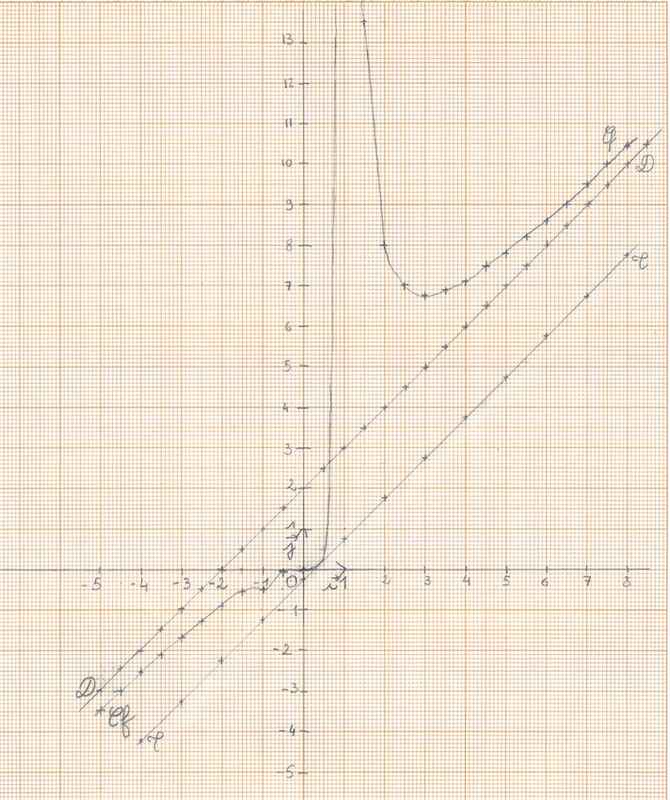
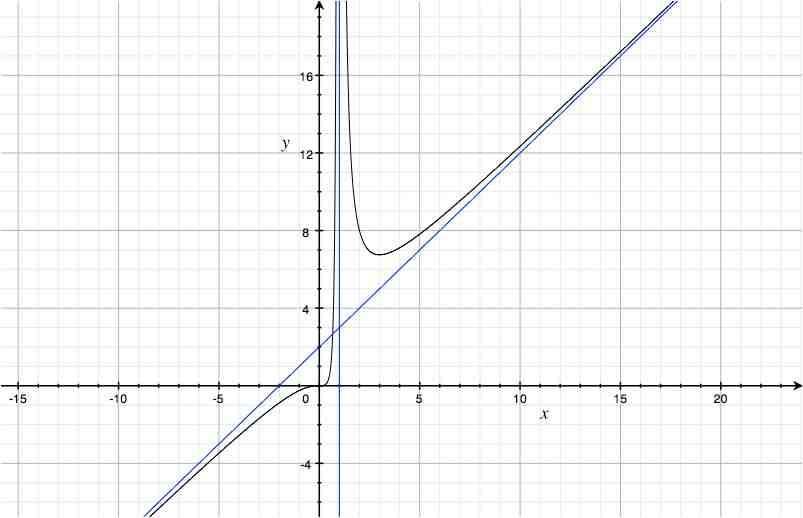
On sait que f(x)= x³/(x-1)², j'ai aussi déjà répondu à des question sur la droite (D): y=x+2 et la tangente (T): y=x-1/4, que j'ai tracées sur la courbe.
5)a)A l'aide du graphique, étudier, suivant les valeurs du paramètre p, le nombre de solutions de l'équation: f(x)=x+p
b) Préciser l'ensemble D des valeurs de p pour lesquelles cette équation admet deux solutions possibles.

Pour la question a), par lecture graphique j'ai trouvé les ensembles suivants:
Si p [ -4; -1/4 [, alors on a pas de solution.
Si p= -1/4, alors on a une solution
Si p ] -1/4; 1,5], alors on a deux solutions.
Si p ] 1,5; 2], alors on a une solution.
Si p ] 2; +], alors on a deux solutions.

En revanche, pour la question b), je ne sais pas trop par où commencer... J'ai essayé de calculer p=f(x)-x, ça me donne p=2x²-x/(x-1)². Mais que faire après?