Bernoulli l'hospital

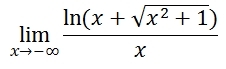
Merci d'avoir répondu si vite, mais je n'ai jamais entendu parler de cette formule...

N'ayant pas fait de cours sur les limites depuis mon lycée, n'y aurait-il pas un moyen plus "lycée" de résoudre cette limite ? J'ai essayé de factoriser, de modifier le ln pour me ramener à une limite connue liée à un taux d'accroissement ou à des croissances comparées mais rien ne fonctionne...

Bonjour,
tu mets x en facteur pour obtenir la limite d'une forme ln(x)/x qui est 0 en +inf.

suivre alors la remarque de tranquilo_22

Bonjour, je vous remercie, mais la limite que je cherche est en moins l'infini, or lim lnx/x en moins l'infini est inconnue je crois.

erreur de ma part, c'est la limite en -infini qu'il faut chercher. J'ai lu un peu vite.
ln(x) n'est définie que sur * donc la limite en -inf n'existe pas

C'est ce que j'ai pensé au début mais x + racine(x²+1) est strictement supérieur à 0 pour tout x de donc j'en ai conclu que la limite existait... Ai-je tord ?

en effet, tu as raison !!
Alors:


pour l'égalité (1), tu fais:

mafiaOfVodka: En effet,

Bonjour

Comme pour tout , on a est positif pour tout , donc on peut bien parler de la limite quand tend vers .



et après on applique des croissances comparées.

En retard...

J'ai compris !

Merci beaucoup pour votre aide, et en plus on trouve 0, ce qui m'arrange grandement pour la suite.
Encore merci !

Je signale que même si ça ne saute pas aux yeux, la fonction est paire!

en effet, et donc et tu peux utiliser la technique de MafiaOfVodka

en et conclure

salut

un moyen lycée ?

pour x < 0

x + (x² + 1) = -x[(1 + 1/x²) - 1]

on prend le logarithme en utilisant ln(ab) = ln(a) + ln(b)

ln(-x)/ x --> 0 quand x --> -oo  (croissance comparée)

le deuxième terme (1/x)ln[1 + ... - 1] est de la forme Xln(X) --> 0 qd X --> 0 qd x --> -oo

par somme la limite est nulle ....