Inscription / Connexion Nouveau Sujet
Formule de Taylor avec reste intégral
Bonjour,
J'ai du mal à démontrer la formule de Taylor avec reste intégral généralisée. Soit de classe
avec
un ouvert de
. Alors, avec
et
:
Je sais bien qu'il faut faire par récurrence, comme pour le cas où d=1 et n=1. Cependant, si est
, j'obtiens par intégration par parties :
L'intégrale de 0 à t est difficile à calculer. Je suis bloqué.
Comment faire ?
Bonsoir
Je te propose de commencer par écrire deux petites modifications de ton énoncé
1) ça donne quoi si je remplace b par a+h ?
2) en plus de ça, ça donne quoi si d = 1 ?
Quand tu auras 2), démontre la par récurrence (ce sera plus simple à comprendre, puisque c'est de la dimension 1).
Et enfin, tu appliques 2) avec la fonction
Bon en fait la formule de mon énoncé est fausse, la bonne est donnée dans l'image en PJ. Cela dit, j'ai parlé trop vite et j'ai un problème pour démontrer cette formule. En effet, quand j'applique 2) à la fonction, on obtient :
où et
A partir de là, je ne vois pas. Les dérivées successives de sont très dures à calculer. Je ne sais calculer que
, qui est le théorème du cours :
Même par récurrence je n'y arrive pas.
Bonjour, si j'ai compris c'est qu'avec la technique ci-dessus tu as du mal a exprimé en fonction des dérivées partielles de
.
Voici une solution qui n'utilise que la formule de ton cours sur les dérivées composées.
On fait par récurrence tu pars de la formule à l'ordre n sur la pièce jointe, regardes juste l'intégrale. Tu poses la fonction où
. Et
le multi indice de taille n.
Donc tu fais une intégration par partie sur l'intégrale .
Tu intègres le terme et tu dérives
. En utilisant la formule de ton cours tu as que
.
Tu utilises une autre formule bien connue pour toute fonction , différentiable tu as
. Et la je te laisse finir les calculs il y a tous les éléments qui apparaissent
Je ne vois pas où tu veux en venir. On a :
où est le vecteur dont les coordonnées sont nulles, sauf la i-ième qui vaut 1.
Lorsque je somme cela sur $\alpha$ je n'aboutis pas et je ne comprends pas comment tu peux conclure par récurrence.
Bonjour, désolé pour la réponse tardive.
Pour la méthode que j'ai proposé, si tu prends l'égalité que tu as obtenu à gauche (il y a une erreur de signe il faut changer les moins par des plus), et que tu multiplies par , il y aura un terme qui marche bien, (celui avec g(0)) l'autre terme est plus pénible à traiter, pour le mettre de la bonne forme je pense qu'il faut faire du dénombrement et faire attention au subtilité d'écriture (comme par exemple pour passer de
, à
, il faut modifier quelque chose dans les sommes car, on peut remarquer que la première écriture prend en compte l'ordre de dérivation, et la deuxième non, or par le théorème de Schwarz, on peut dériver dans n'importe quel ordre et on aura le même résultat, mais alors pour écrire proprement l'égalité il faut compter le nombre de multi indice "
" et "
" qui donne le multi indice "
et modifier la somme en conséquence).
Plutôt que de se casser la tête avec ça, c'est plus facile de revenir à la première méthode, où tu te ramène à la dimension 1 en introduisant .
Pour calculer tu peux admettre la formule qui est valable pour tout k,
.
Si tu veux démontrer cette formule, tu peux remarquer que . Et donc dériver k fois
c'est la même chose que d'appliquer l'opérateur
k fois à
qu'on évalue ensuite en
en gros tu as la formule
.
Et tu peux alors montrer par récurrence le "binôme de newton généralisé avec la notation multi indice" (formule valable sur tous les anneaux commutatifs)
.
(La récurence se fait sur et pour d=2 tu retrouves le binôme de newton).
mais alors pour écrire proprement l'égalité
Je voulais dire pour faire le changement de variable proprement plutôt*.
Pour la première méthode que j'ai proposé on peut procéder de cette façon :
On insère la partie gauche de ton égalité avec le reste,
comme j'ai dit plus haut le terme problématique est :
Qui est égale à :
Jusqu'ici pas de problème d'après la remarque que j'ai faite plus haut il y a plusieurs couple qui forme le même multi indice
c'est important de s'en rendre compte pour le changement de variable.(Par exemple (2,2,1)= (1,2,1)+ (1,0,0)= (2,1,1) + (0,1,0)...) On veut pouvoir poser
. La fonction
est une surjection de
où
est l'ensemble des multi indice de taille i. Si on se donne
un multi indice de taille n+1, on veut connaître les couples
tel que
. En fait ce sont tous les couples de la forme
(quand c'est possible de retirer 1 à la coordonnée i). Donc en gros un terme du type
se transformera après changement de variable en
. (On préfère la deuxième écriture car il n'y a plus besoin de faire attention à si on peut enlever 1 à la coordonnée i). Après changement de variable la somme s'écrit alors :
. Mais comme
, on a
, donc la somme est égale à
. Et on peut terminer la récurrence.


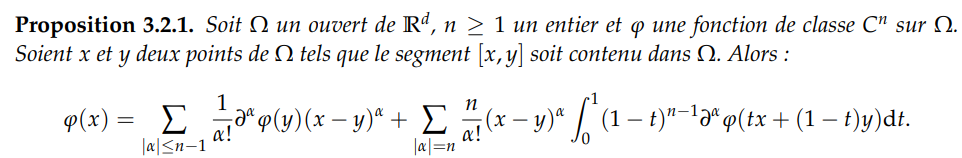

 analyse en post-bac
analyse en post-bac