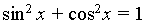
...par l'équation du cercle unité

avec x=cost et y=sint

x²+y²=1

Philoux

Ok mais je pensais aux autres formules telles que :

cos(a+b)
cos(a-b)
sin(a+b)
etc....

Avez-vous des astuces pour les retrouver ?

Tu peux toujours repasser par les exponentielles mais vive la galère.
Moi même je ne connais pas toutes mes formules mais celle que tu as écrites, c'est le minimum.

Une méthode pour trouver cos(p)+cos(q)  (ou cos(p)+sin(q)...)
On pose a=(p+q)/2 b=(p-q)/2
On a alors a+b=p et a-b=q
Et à l'aide des formules que je te conseille de connaître on retrouve la formule.
Par contre c'est nul quand tu es en colle et que le prof te presse pour que tu sortes la formule sur le champ ^^ (exp inside)

par les exponentielle c'est tres simple si on si prend bien.


par exemple: cos(a+b)= Re(exp(a*i)*exp(i*b)) = cos(a)*cos(b)-sin(a)*sin(b)



sinon, oui toute les formule ce retrouve par le calcule vectorielle ou autre... a condition de savoir qu'elles existent aussi ^^

Pour retrouver les relations de manière plus géométrique (mais c'est pas très évident, faut reconnaître), on peut se servir de la figure ci-jointe.

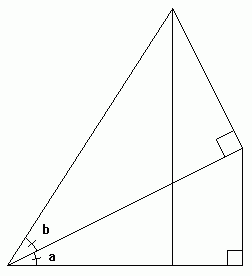
Comment trouves-tu par exemple sin(2a) avec cette figure ?

en prenant b=a et en donnant l'expression de l'ordonnée du sommet...

Philoux

Et on retrouve la formule littérale 2.sina.cosa ?
Peux-tu reprendre la figure avec des annotations pour m'expliquer ?

Merci d'avance