Inscription / Connexion Nouveau Sujet
Géométrie dans l'espace. Cube et tétraèdre.
Bonjour à tous !
J'ai un exercice à faire pour la rentrée, j'ai presque fini sauf la dernière question..
Je vais vous mettre tout l'énoncé comme ça vous pourrez peut-être m'aider.
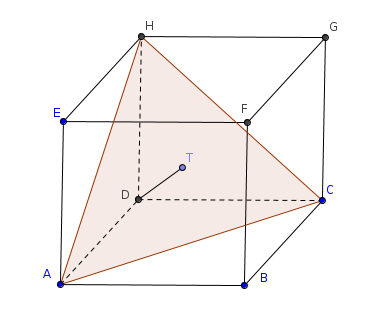
ABCDEFGH est un cube d'arête 6 cm.
1.a. Quelle est la nature du triangle HAC ?
b. Tracer ce triangle en vraie grandeur.
c. Combien vaut son périmètre ?
Combien vaut son aire ?
2. Calculer le volume du tétraèdre DHAC.
3. Déduire des questions précédentes la hauteur du tétraèdre DHAC relativement à la base HAC.
(voir figure : le triangle HAC est en rouge)
J'ai déjà répondu à :
1.a. HAC est un triangle équilatéral car AC = AH = HC diagonale d'une face du cube.
b. D'après le théorème de Pythagore dans le triangle ABC :
AC2= AB2+BC2=62x2 (=72)
AC = 6
2
c. Le périmètre du triangle ACH est :
62 x3 = 182 cm
L'aire du traingle ACH est 62 xh/2
AH2= (CH/2)2+h2 d'après le théorème de Pythagore
h2= (62)2-(32)2
= 36 x 2 - 9 x2
= (36-9)x2
= 54
h = 54 = 36
L'aire est :
(62 x36)/2 = (3x2x2x3x2x3)/2
= (18x23)/2
= 183
2. Volume de OHAC :
V = 1/3 x B x h
= 1/3 x 62 x 36
= 1/3 x 36 3
= 123 cm3
Voilà .. et je bloque sur la dernière question .. 
Merci si vous pouvez m'aider..
Rappelle-moi le volume du tétraèdre ?
et quelle base as-tu choisie pour le calculer ?
n'y a-t-il pas une solution plus simple ?
Pour la deuxième question c'est :
V = 1/3 x B x h
B = Aire de AHC = 183
V = 1/3 x 183 x h
Comment on fait pour h ? c'est la même que pour un triangle ?
mais non
tu connais la hauteur du tétraèdre ACDH de BASE ACD
c'est 6
Ensuite on change de perspective, on te demande la hauteur du même tétraèdre, mais en prenant cette fois pour BASE ACH
On calcule le volume de deux manières différentes
la première donne sa valeur, car on connait toutes les mesures (base ADC et hauteur DH)
la seconde fait intervenir une inconnue : on connait la base ACH, mais pas la hauteur [DT]=h.
Mais grâce au premier calcul, on a une égalité qui permet d'obtenir cette nouvelle hauteur h
tu as compris ? tu as fait tilt, oui 
surface de ADC ?
hauteur [DH] ? 6
volume tétraèdre ACDH, de base ACD, de hauteur [DH] ?
ACH est équilatéral. On peut démontrer que la surface d'un triangle équilatéral de coté a est
surface de ACH ?
hauteur [DT] ? h, l'inconnue
volume tétraèdre ACDH, de base ACH, de hauteur [DT] ?
Mais ce volume est le même, quelle que soit la méthode de calcul, donc
Il te reste à trouver h.
J'ai pas très bien compris cette partie là :
" ACH est équilatéral. On peut démontrer que la surface d'un triangle équilatéral de coté a est 3/4
2
surface de ACH ? 3/4x(62)2= 183
hauteur [DT] ? h, l'inconnue
je dois y aller.. Tu peux me répondre, je verrai la réponse tout à l'heure.
Merci beaucoup de m'avoir aidé ! 
à te rappeler une formule à connaitre concernant l'aire d'un triangle équilatéral.
tu peux me dire d'où tu sors la valeur
B = Aire de AHC = 183
de ton message de 10:15 ? 
Géométrie dans l'espace. Cube et tétraèdre.
Annuler
connectez vous