Bonjour

le manque de rigueur ne pardonne pas en maths

Quelle est la nature de la section ? de quelle section ??? énoncé dans lequel il en manque un bout !

on devine plus tard que il s'agirait de la section par le plan (IJK) !!

ta conjecture est correcte
mais un coup tu parles de triangle équilatéral un coup tu parles de triangle rectangle !! faudrait savoir !!
et de que(s) triangle(s) tu parles (noms)

pour la preuve il ne s'agit plus de "constater" (ça c'est pour la conjecture) mais de justifier
oui les points I,J,K sont sur certaines diagonales à préciser
or ces diagonales définissent un plan (lequel : son nom) qui contient par conséquent les points I,J,K et donc est le plan de coupe (IJK)
et une fois qu'on a ainsi identifié clairement ce dont on parle et de quels segments précisément est constituée la section, il ne sera pas bien compliqué de justifier que des diagonales de carrés égaux sont égales !

Je suis désolé, je n'avais pas relu avant de poster. Et je vais essayer d'être plus rigoureux.
Ce que vous dites est tout à fait évident, pourtant j'ai oublié de l'écrire avant de poster, désolé.

Je parlais bien d'un triangle équilatéral et non rectangle
Les diagonales où se situent en leur milieu les points I, J, K, sont (AF) et (EB), (CF) et (GB), (HF) et (EG).
Mais je ne suis pas sûr d'avoir compris ce que vous disiez (et je ne veux pas dire de conneries donc je préfère demander), quand vous dites : [ "or ces diagonales définissent un plan (lequel : son nom)  qui contient par conséquent les points I,J,K et donc est le plan de coupe (IJK) "].
Les carrés ABFE, BCGF, EFGH étant égaux, on peut alors en déduire que les diagonales de ces carrés sont égales.
Par conséquent, le triangle IJK est un triangle équilatéral.

(AF) et (EB) oui mais une seule est utile !!!
l'autre ne sert à rien du tout et en particulier n'a rien à voir avec la section demandée. idem sur les autres faces
quand tu auras identifié clairement les diagonales qui servent et envoyé aux oubliettes celles qui ne servent à rien, tu comprendras de quel plan je parle (quel est son nom en référence au cube seul ABCDEFGH).

D'accord, donc on utilise les diagonales (AF), (FC) et (HF) ?

aucun rapport.

il semble même que tu n'aies fait aucune figure pour sortir de pareille bourdes
on se demande bien d'où tu sors ta conjecture alors ...

C'est sans doute parce que j'ai mal nommé les points ou alors c'est que je ne vois pas...

Ah je comprends mieux !!
ce que tu ne vois pas et qui fait en fait que ta conjecture n'est absolument pas ce que tu pensais,
(résultat de trucs flous dès le départ par absence de précision exacte sur quel triangle dont tu parles, un triangle ce n'est pas "le triangle épicétou" mais son nom exact, les noms exacts et précis de ses sommets !! entrainant un dialogue de sourds)

et donc que tu ne risques pas de pouvoir la démontrer, et que tu comprends ce que je dis de travers et vice versa (dialogue de sourds dis-je), est que la section du cube n'est absolument pas le triangle IJK mais ça :

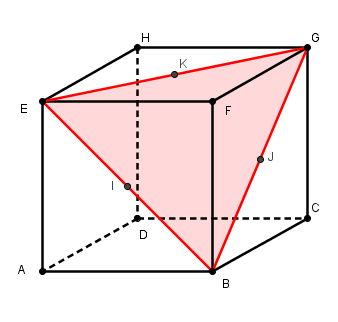
Je suis clairement idiot...
Désolé de vous avoir fait perdre autant de temps à cause de mon erreur
Et croyez moi que maintenant c'est bien ancré dans ma tête !

Maintenant je comprends mieux : les diagonales sont donc (EB), (BG), (GE) et elles définissent le plan (GBE).
Donc c'est le triangle GBE qui est équilatéral

voila !

Merci beaucoup pour votre aide

BenCelier, je te mets un lien vers l'autre sujet, si tu désires le poursuivre
Géométrie

ah, c'était le même posteur ...

ils ne se rendent pas compte qu'ils perdent en qualité d'aide en agissant ainsi...
là, on connait le contexte, on sait qu'il bosse, autant pouvoir suivre l'évolution de ses connaissances...