Je bloque sur un exercice que voici:

ABCD est un carré de sens direct de coté 1. On trace les triangles équilatéraux BCE et DCF respectivement à l'intérieur et à l'extérieur du carré comme indiqué sur la figure ci-dessous.



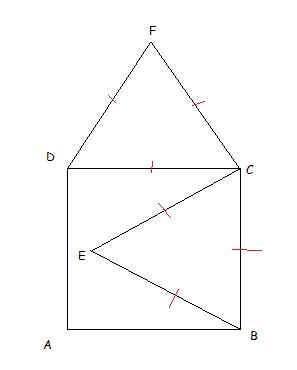
1) Quelle conjecture peut-on émettre pour les points A,E et F ?

--> Alignés

2) déterminer les affixes a, b, c, et d des points A, B, C et D dans le repère orthonormé direct (A;AB;AC)[vecteurs], e est l'affixe du point E et Z le nombre complexe:

Z= (e-c)/(b-c)

--> a=0 b=1 c=1+i d=i

3) a) Déterminer une mesure de l'angle (CB, CE)[vecteurs].

On peut voir graphiquement que l'angle est de 60% car c'est un triangle équilatéral donc 180/3. Cependant on cherche plutôt la réponse -/3, qu'on peut trouver grâce au cours mais seulement si on connaissait e ! Et vu que je ne sais pas comment trouver e alors je ne peux pas donner la bonne mesure de l'angle.

b) Déterminer la valeur du quotient (CE)/(CB).

Là je ne vois pas trop ce qu'il demande, vu que ce ne sont pas des vecteurs car c'est bien écrit sans la petite flèche alors j'ai tendance à répondre: 1/1=1 ? D'où l'inutilité de cette question pour la suite.

c) Déduire ce qui précède une forme exponentielle de Z, puis la forme algébrique de e.

Sans e je ne peux pas trouver ne serait-ce que le module de Z d'ailleurs ils nous demande la forme algébrique de e.

4) Proposer une méthode permettant de déterminer la forme algébrique de f affixe du point F

Cette méthode doit être la même que pour trouver e donc je ne vois pas

5) a) Déterminer l'affixe du vecteur AE, puis celle de AF.

Pour cette question j'peux continuer si j'ai l'affixe e et f.

b) Démontrer la conjecture émise à la question 1)

J'peux le faire aussi par rapport à la question précédente.