Inscription / Connexion Nouveau Sujet
géométrie et nombre complexes
Bonjour, impossible de résoudre cette exercice après des heures à avoir essayer plein de méthode.
Soit z
U/{1}. On considère les points A(1+z) et B(1-z). Montrer que les droites (OA) et (OB) sont perpendiculaires.
Il faut que l'argument de OA et OB soit un imaginaire pur mais il nous manque le point. Aucun calcul concluant avec de nombreuse valeurs de O différentes :
O(x+iy), O(x'+iy'),O(x0;y0),O(0;0)
Pour compléter :
Si, dans un repère orthonormé, deux vecteurs et
ont pour coordonnées
et
donc pour affixes
et
, on a :
Bonjour et merci de votre réponse,
cependant je ne vois pas le lien entre les points A et B ainsi que (1+z)(1-\bar{z}) (qui ne me semble pas un imaginaire pur d'ailleurs).
Il faut montrer que arg(zB-zO/zA-zO)
/2{2}
Il faut montrer que arg(zB-zO/zA-zO)
/2{2}C'est une autre solution, oui.
Autrement dit,en supposant
Autrement dit encore :
Compte tenu que
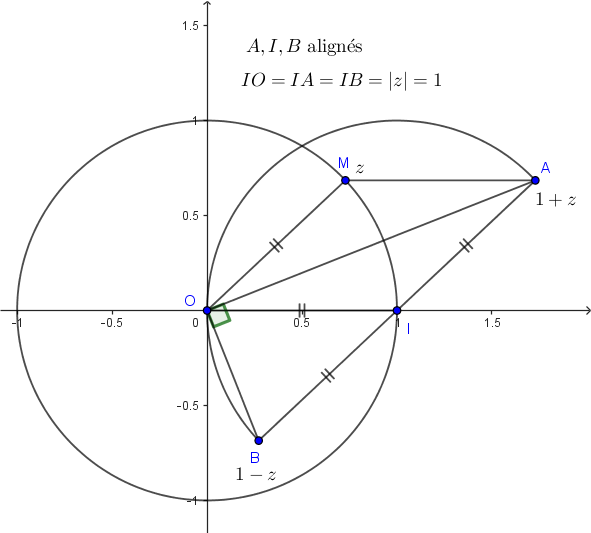
Au fait, il existe aussi un argument géométrique :
Les diagonales d'un losange sont perpendiculaires.
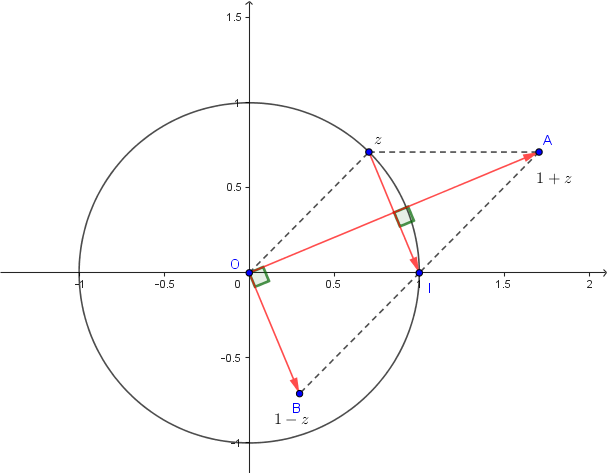
Je reviens sur ceci :
cependant je ne vois pas le lien entre les points A et B ainsi que (1+z)(1-\bar{z}) (qui ne me semble pas un imaginaire pur d'ailleurs).
et pourtant :
salut
le vocabulaire laisse à désirer :
Il faut que l'argument de OA et OB soit un imaginaire pur mais il nous manque le point.
il suffit qu'une mesure de l'angle orienté (OA, OB) soit pi/2 mod pi
donc que le quotient des affixes des vecteurs OA et OB soit imaginaire pur
puisque multiplier par un nombre complexe w revient (à homothétie près) à faire tourner un vecteur de l'angle arg (w)
et pour le résultat de lake remarquer alors que
Bonjour rttgtry,
d'après ton premier message tu n'as pas l'air d'avoir compris que O désigne l'origine du repère.
Ensuite pour parler des droites OA et OB il faut supposer z différent de 1 et de -1.
Enfin cet exercice est immédiat si on pose (qui vérifie
) :
puisque le vecteur OA a pour coordonnées et le vecteur OB a pour coordonnées
le produit saclaire de OA par OB vaut
.
OK merci beaucoup, j'ai tout compris!
Mon incompréhension venait du fait que j'avais totalement oublié que zU/{1} et donc que |z|=1.
Il faut bien lire l'énoncé!
Oui, cela arrive à tout le monde de lire un peu vite un énoncé et de sauter une information importante.
Annuler
connectez vous
algèbre en post-bac