Bonjour,

Soit une relation d'équivalence sur un ensemble . Par construction même, l'application est surjective. Pourrait-il exister un point dans n'ayant aucun antécédent dans par ? Pourquoi ?

Avec tout mon respect,

T. P.

bonjour thierry,
en effet, non ?
merci

Green,

D'une part, il est faux d'asserter que , vu que et, même si tu m'avais écrit ça, cela n'aurait pas constitué la raison. Alors, pourquoi ?

T. P.

En fait, je n'ai jamais vu les groupes (où est une relation d'équivalence), je ne connais que les groupes où E et H sont des groupes.
Au fait, je ne vois pas trop à quoi correspondent concrètement les classes d'équivalences pourrais tu m'en dire un peu plus s'il te plait ?
merci
PS: tu vas bien ?

Bonjour

Je me demande bien comment tu peux parler de "classes d'équivalence", si tu ne sais pas quelle est la relation d'équivalence associée...

Un élément de E/H, c'est une classe de H dans E, c'est-à-dire un sous-ensemble de E de la forme xH, où x est un élément de E. Il est bien évident que toute classe xH aura x comme antécédent par la projection canonique. (Quels sont les autres ?)

Un schéma :



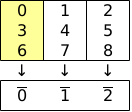
En haut le groupe des entiers modulo 9. Il est abélien, donc tout sous-groupe est distingué. En jaune, le sous-groupe . Chaque colonne est une classe d'équivalence pour la relation définie par si et seulement si . En bas le groupe , et les flèches inidquent la projection canonique : claque classe d'équivalence est envoyé sur un élément de .

Et on remarque que chaque classe d'équivalence est bien de la forme , pour un certain élément de . Autrement dit, la relation peut également se définir ainsi : si et seulement si il existe tel que . On dit que sont congrus modulo un élément de , voire simplement "modulo ".

ah ok, je commence en effet à comprendre
je réfléchi encore un peu sur le post et reposterais si besoin
merci

Je vais assez bien, je te remercie beaucoup. Et toi ?

Je te parle en toute généralité, sans viser particulièrement les structures de groupes, d'espaces vectoriels, d'algèbres ou encore topologiques, pour ne parler que de celles-là. Soit un ensemble et une relation d'équivalence sur (i.e. une relation binaire sur réflexive, symétrique et transitive). Pour un élément quelconque fixé dans , l'idée fondamentale est de regrouper dans un seul et même sous-ensemble de tout élément dans tel que . La notion de sous-ensemble d'équivalence est donc née et l'on pose habituellement que (ou bien , ...). Tu l'auras intuitivement compris, si est tel que , alors , d'où (Tu peux me montrer cette identité !). L'autre idée est de ranger (ou classer) ces nouveaux objets dans un nouvel ensemble, que l'on note habituellement ou bien , ensemble qui est tel que par construction. Chaque point de s'appelle une classe d'équivalence modulo (ou simplement "classe d'équivalence" si aucune confusion n'est à craindre).

Par réflexivité de , l'on a pour quelconque dans , de sorte qu'aucune classe d'équivalence n'est vide. D'autre part, il est clair que, pour tout dans , , de sorte que . L'inclusion réciproque est évidente. Enfin, si l'on prend et dans telles que , cela implique l'existence d'au moins un dans tel que et et, par symétrie et transitivité, , d'où . Ainsi les classes d'équivalence de sont-elles deux à deux disjointes, si bien que l'ensemble forme une partition de . Ce résultat est fondamental, car il permet de mieux comprendre pourquoi l'application est surjective. Finalement, pour clôturer ce petit tour d'horizon, l'on notera l'équivalence et, ce que j'appelle quotient, c'est le couple .

Cette vision des choses est loin d'être exacte (j'en ai une tout autre !) ; mais elle a le seul mérite de mieux concevoir les relations d'équivalence sur un ensemble donné. Dès lors, rien n'empêche de munir d'une certaine structure et, sous des conditions bien précises, de faire en sorte que le quotient soit muni de la même espèce de structure, où devient alors un morphisme selon cette espèce de structure (ex. : un morphisme de groupes en liaison étroite avec les sous-groupes normaux (ou invariants), ...).

Est-ce plus clair ? Je t'en prie, n'hésite pas à me le dire et je te répondrai quand je trouverai le moment. Mais il faut impérativement maîtriser cette notion. Elle est fondamentale en Mathématique.

Avec tout mon respect,

T. Poma

Errata : Lire :

Citation :
La notion de sous-ensemble d'équivalence est donc née et l'on pose habituellement que (ou bien , ...).