Ah oui, j'ai oublié de faire la même chose pour le minimum

Bonsoir

l'idée de ta démonstration est bonne
mais il reste à démontrer qu'une fonction strictement monotone est injective, c'est encore plus simple

Merci beaucoup , je doutais de sa valeur de verité

je viens de relire un coup, et ce que tu affirmes ici est faux

Oui c'est bien ça, elles sont larges mais on peut éliminer l'égalité car f ne peut pas etre constante et injective. Et concernant le deuxième  point je voulais dire par ça qu'il existe un d avec  f(d) le max de l'intervalle f(]a,c[)

J'ai utilisé le TVI pour dire qu'il existe un max dans f(]a,c[)

En d'autres termes cela donna , f(d)>f(xn) avec quelque soit xn ∈[a,c]

je vois, mais je trouve que le fait d'introduire d est un peu casse-gueule, tu te retrouves à faire plusieurs TVI

Si on a alors la valeur est rencontrée deux fois distinctement : une fois sur ]a,b[ et une fois sur ]b,c[
d'où l'absurdité

edit :  

d'ailleurs, l'existence de d n'est pas donnée par le TVI, mais plutôt par le théorème des valeurs extrêmes (il a plein de noms : )

Merci infinimentZormuche

L'utilisation du TVI ets fausse ? car j'ai intuitivement déduis que puisque f(b)>max(f(a),f(c))
donc s'il y a un max c'est sois qlq plus grand que f(b) ou c'est f(b)

Je te décris ce qui se passe sans aucun max ni min. C'est long, y'a beaucoup de mots, mais ce n'est que du TVI et de l'injectivité


Puisque f est injective, quitte à considérer -f à la place, on peut trouver a<b tels que f(a)<f(b).
Alors la fonction ne peut être que strictement croissante sur [a,b].

En effet, si la continuité et le TVI nous disent que f prend toutes les valeurs entre f(a) et f(x) et toutes les valeurs entre f(x) et f(b). Alors, toujours selon le TVI, il est impossible que f(x)<f(a) sinon f(a) serait une valeur intermédiaire entre f(x) et f(b) et il existerait tel que f(y)=f(a) et donc y=a par injectivité. Absurde puisque y>x>a. De même, impossible que f(x)>f(b). Puisque x est différent de a et b, son image est différente de f(a) et f(b) et donc f(a)<f(x)<f(b). Si z est un élément de , le même raisonnement avec x à la place de a et z à la place de x nous dit que f(x)<f(z)<f(b) et donc f est strictement croissante sur [a,b].

Soit y>b, alors il est impossible que f(y)=f(b) (sinon y=b) et impossible aussi que f(y)=f(a).
Supposons que f(y)<f(b). Si f(y)<f(a) alors f(a) est une valeur intermédiaire entre f(y) et f(b). Donc il existe tel que f(z)=f(a) et donc z=a alors que z>b>a. Absurde.
Donc f(a)< f(y) <f(b). Donc f(y) est une valeur intermédiaire entre f(a) et f(b). Donc il existe z entre a et b tel que f(z) = f(y), ce qui implique z=y < b. Contradiction. Ainsi f(y)>f(b).
Le même raisonnement montre que tout élément inférieur (strictement) à a possède une image (strictement) inférieure à f(a).

Soient maintenant x!=y. On suppose sans perte de généralité que x<y.
Si x<=b alors ou bien y<=b et donc f(x)<f(y) par croissance sur [a,b], ou bien y>b et donc f(y)>f(b)>=f(x) et même conclusion.
Si x<=a et y>a alors f(x)<=f(a) < f(y) d'après ce qui précède, que y>b ou non.
Si x<y<a, il est impossible que f(y)<f(x), sinon f(x) est intermédiaire entre f(y) et f(a) et donc il existe z\in]y,a[ tel que f(z)=f(x), puis x=z alors que z>y>x. Donc f(x)<=f(y) puis f(x)<f(y) par injectivité.
De même, si b<x<y, alors impossible que f(x)>f(y) sinon f(y) est intermédiaire entre f(b) et f(x) donc il existe tel que f(z)=f(y) puis z=y  et y>x contredit z<x.
Ce qui prouve la stricte croissance de f ou -f sur R tout entier, i.e la stricte monotonie de f.

Maintenant je résume les étapes avec des mots

1) Trouver a et b d'images différentes et choisir de travailler avec f ou -f de sorte à avoir a<b et f(a)<f(b)
2) Montrer la stricte croissance sur [a,b]. Exactement la même preuve montre au passage que f est strictement croissante sur n'importe quel intervalle [s,t] avec s<t dès que f(s)<f(t)
3) Montrer que z>b implique f(z)>f(b) et symétriquement, que z<a implique f(z)<f(a)
4) Se donner x<y et coincer majorer l'un ou l'autre : par exemple si y<a, alors d'après 3) on a f(x)<f(a). On applique ensuite 2) avec s = x et t = a pour en déduire f(x) = f(s)<f(y)<f(t)=f(a).

Merci infiniment c'est bien détaillé

Est-ce que ma démonstration est totalement fausse ? Pour savoir si je dois changer de voie de réflexion

C'est pas faux, et tu peux conserver les inégalités strictes au début.
Il est impossible que f(b) = max(f(a),f(c)), sinon f(b) = f(a) ou f(b)=f(c), donc b=a ou b=c, ce qui contredit a<b<c. Idem pour le min. Tu décides de ne traiter qu'un cas et de dire que l'autre se traite pareil (ce qui revient à choisir de travailler avec f ou -f, puisque -max(-.) = min(.)).
Ensuite tu peux faire tout d'un coup : il existe un élement d strictement entre max(f(a),f(c)) et f(b) (et son image est par injectivité différente de f(a) et f(c)).
Aussi, min(f(a),f(c))<max(f(a),f(c)) puisque f(a)!=f(c). Donc il existe un autre élement e<d strictement compris entre le min et le max tel que f(e) soit différent de f(a) et f(c).

Donc il existe par le TVI un élement x entre d et e tel que f(x)=max(f(a),f(c)). Donc x = a ou c.

Ulmiere MILLE MERCI

mais comme je l'ai dit, on peut effectivement se passer des égalités puisque sinon f est trivialement non injective

      Une autre façon de faire  ( mais qui utilise la notion de connexité ):
     Soient  I un intervalle non vide de et f : I continue .
Soient  V  := { (x ,y) ² │ x < y } et W :=  { (x ,y) ² │ x >y }   .
V et W sont des ouverts de ² .
F : (x , y) (f(x) , f(y)) est continue de I² vers ²    donc  F^-1(V)et F^-1(W) sont des ouverts de I² .

Si f est injective  I² = F^-1(V) 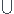F^-1(W) .
I² étant connexe  F^-1(V) = I²  (donc f est strictement croissante ) ou , sinon ,  F^-1(W)  = I²  ( et   f est strictement décroissante )

etniopal j'aime beaucoup cette façon

Bonjour !
Un peu comme etniopal mais sans utiliser la notion de connexité, seulement celle de convexité.

Soit et définie sur par .

est convexe car
c'est un demi-plan si
intersection de deux demi-plans si est majoré ou (exclusif) minoré
intersection de trois demi-plans si majoré et minoré.

Pour on a donc .
Si on a continue sur et l'image de est donc un intervalle.
Comme ne s'annule pas (puisque injective) les valeurs sont de même signe et strictement monotone.