Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieur AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau école ingénieur
Partager :

Intégral par le Théorème de Résidus 1

Posté par
Mathes1 29-10-23 à 11:44

Bonjour à tous
J'ai un exercice merci beaucoup d'avance
2) Évaluer l'intégrale (Théorème de Résidus) suivants:
J_1=\int_{0}^{2\pi}\dfrac{1}{2+sin(\theta)} d\theta
Alors je propose :
Pour évaluer l'intégrale J_1 = \int_{0}^{2\pi}\dfrac{1}{2+\sin(\theta)} d\theta en utilisant le théorème des résidus, on a:

1. On identifie les pôles de la fonction \dfrac{1}{2+\sin(\theta)}. Les pôles se produisent lorsque le dénominateur s'annule, c'est-à-dire lorsque \sin(\theta) = -2. Cela se produit lorsque \theta = \arcsin(-2). Cependant, \sin(\theta) varie dans l'intervalle [-1, 1], donc il n'y a pas de solution réelle pour \arcsin(-2). Cela signifie qu'il n'y a pas de pôles à l'intérieur du contour d'intégration.

2.on  applique le théorème des résidus modifié, qui stipule que si une fonction analytique est définie à l'intérieur d'un contour fermé et ne contient pas de pôles à l'intérieur de ce contour, alors l'intégrale le long du contour est nulle. Dans ce cas, puisqu'il n'y a pas de pôles à l'intérieur du contour [0, 2π], l'intégrale J_1 est nulle.

Donc, J_1 = 0.
Merci beaucoup d'avance !

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 29-10-23 à 12:10

Bonjour,

J_1= \dfrac12 \int_0^{2\pi}\dfrac1{1+0,5 sin(\theta)} d\d\theta

Posté par
Ulmierere : Intégral par le Théorème de Résidus 1 29-10-23 à 12:48

Pour tout \theta réel, 2 + \sin\theta \leqslant 3, donc J_1 \geqslant \dfrac{2\pi}{3} > 0. Ton résultat n'a pas de sens

Par contre, le 2+\sin complexe peut s'annuler et est même non bornée, vue comme fonction de la variable complexe.

\sin(re^{it}) = Im(e^{ir\cos t - r\sin t} ) = e^{-r\sin t}\sin(r\cos t)

Posté par
Ulmierere : Intégral par le Théorème de Résidus 1 29-10-23 à 13:33

Voilà que je me contredis à mon tour
Mon calcul n'est vrai que pour r = 1.

Pour r quelconque, ce n'est plus la partie imaginaire et du coup

\begin{array}{lcl} \\ 2i\sin(re^{it}) &=& e^{-r\sin t}(\cos(r\cos t) + i\sin(r\cos t)) - e^{r\sin t}(\cos(r\cos t) - i\sin(r\cos t))\\ \\ &=& -2\sinh(r\sin t)\cos(r\cos t) + i2\cosh(r\sin t)\sin(r\cos t) \\ \end{array}

donc 2 + \sin(re^{it}) = 2\left[1 + \cosh(r\sin t)\sin(r\cos t) + i\sinh(r\sin t)\cos(r\cos t)\right]

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 29-10-23 à 14:57

On peut aussi voir les choses ainsi :

Comme l'angle θ varie entre 0 et 2π, on le prend comme l'argument de l'affixe z d'un point situé sur le cercle unité C centré à l'origine :

z = e^{i\theta} , 0 \le \theta < 2\pi

\sin(\theta)=\dfrac{z - z^{-1}}{2i}

L'intégrale  est alors l'intégrale de contour d'une fonction de z sur le cercle C parcouru dans le sens direct.

\oint\limits_{C}\dfrac 1 {z^2+iz-1}dz

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 29-10-23 à 15:07

autre chose : J1 ne vaut pas 0

Posté par
Mathes1re : Intégral par le Théorème de Résidus 1 30-10-23 à 14:02

Bonjour
Je trouve que :
J_1=\int_{0}^{2\pi}\dfrac{1}{2+sin(\theta)}d\theta=\int_{0}^{2\pi}\dfrac{2}{4+i\left(\dfrac{1}{z}-z\right)} dz
Je trouve pas votre formule
Merci beaucoup

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 30-10-23 à 16:34


je pense que vous avez oublié que :

z = e^{i\theta}   , donc,     dz=i e^{i\theta} d\theta =izd\theta

donc,

d\theta =\dfrac{dz}{iz}

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 30-10-23 à 16:46

j'ai également une erreur de recopie : au numérateur c'est 4iz et non iz.
Je vous prie de bien vouloir m'excuser.

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 30-10-23 à 16:53

et le numérateur vaut 2. (sorry, je ne sais pas recopié ce que je fais).

Posté par
Mathes1re : Intégral par le Théorème de Résidus 1 30-10-23 à 17:52

Bonjour
Oui effectivement je suis désolé pour cette erreur,
Et oui je trouve :
\int_{1}^{1} \dfrac{2}{4iz+z²-1}
Et les bornes sont étrange

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 30-10-23 à 18:53

Il ne s'agit pas d'un changement de variable classique, vous êtes dans les complexes.  Vous faites l'intégrale sur la contour  C qui est le cercle unité parcouru  le sens direct et par la méthode des résidus.


\oint\limits_{C}f(z)\mathrm{dz}=2i\pi\sum_1 ^n Res_f(z_i)

avec zi les pôles de f(z).

Posté par
Mathes1re : Intégral par le Théorème de Résidus 1 30-10-23 à 20:53

Bonjour
Je trouve :
*Res(J_1,(-2-\sqrt{3})i)=\dfrac{\sqrt 3}{3}i
*Res(J_1,(-2+\sqrt 3)i)=-\dfrac{\sqrt 3}{3}i
Donc on choisit le Complexe Positif Et pourquoi merci beaucoup

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 30-10-23 à 21:38


remarques :
1)ce n'est pas Res(J1, ..) mais Res(f(z),..)
2)il faut additionner les résidus et multiplier par 2i\pi)
3) vous avez oublié une chose sans doute écrite dans votre cours.

Je m'explique :
Vous avez bien trouvé les 2 pôles de f(z) à savoir :

p_1=-2-i\sqrt{3}    et   p_2=-2+i\sqrt{3}

donc :

f(z)=\dfrac2{(z-p_1)(z-p_2)}

petit rappel : les résidus pris en compte pour la résolution par la méthode des résidus sont ceux qui sont dans le cercle unité.
Alors p_1 et p_2 sont où par rapport au cercle unité?
Vérifiez et revoyez votre calcul ( et votre cours aussi).

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 30-10-23 à 21:54

erratum :  p_1=-2-\sqrt{3}  et    p_2=-2+\sqrt{3} , il n'y as pas de i bien sûr. (encore une erreur de copie, sorry)

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 30-10-23 à 21:57

annule et remplace,je ne suis pas en forme ce soir.

p_1=i(-2-\sqrt{3})    et     p_2=i(-2+\sqrt{3})

Posté par
Mathes1re : Intégral par le Théorème de Résidus 1 30-10-23 à 22:07

Bonjour
D'abord c'est

Citation :
\red{p_1=(-2-\sqrt{3})i} \\et   p_2=\red{(-2+\sqrt{3})i}

p1 et p2 appartient au cercle unité [0,2π]
Merci

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 30-10-23 à 22:12

vous êtes sûr, faites un dessin.

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 30-10-23 à 22:13

autre chose: le Contour est le cercle unité du plan complexe.

Posté par
Mathes1re : Intégral par le Théorème de Résidus 1 31-10-23 à 18:34

Bonjour
L'intégrale J1 est bien nulle
Car sa primitive par la méthode usuelle est : \dfrac{2}{\sqrt 3}arctan\left(\dfrac{2}{\sqrt 3} tan\left(\dfrac{x}{2} \right)+\dfrac{1}{\sqrt 3}\right)
On remplace par 2\pi et 0 on trouve 0 .
Donc les deux résidus sont inclus
Merci

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 31-10-23 à 20:03

Un des deux pôles n'est pas à l'intérieur du contour C.

vos 2 pôles sont des imaginaires purs.
Dans le plan complexe, la partie réelle est sur l'axe des x et la partie sur l'axe des y.

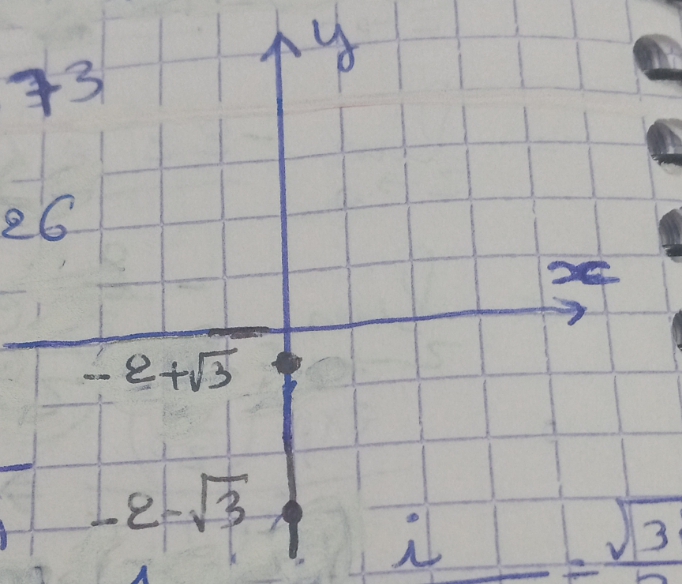
Faites le plan tracé le cercle et placez les pôles.

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 31-10-23 à 20:38

autre chose; je maintiens que J1 ne vaut pas 0.

Pouvez-vous me faire part de la méthode usuelle que vous avez utilisez et comment vous avez conduit le calcul pour trouver votre résultat.

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 31-10-23 à 20:39

Dans le plan complexe, la partie réelle est sur l'axe des x et la partie imaginaire sur l'axe des y ( axe i)

Posté par
Mathes1re : Intégral par le Théorème de Résidus 1 31-10-23 à 20:57

Bonjour
Intégral par le Théorème de Résidus 1
la méthode utilisé
Merci

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 31-10-23 à 21:04

Oui c'est cela.
le contour C est  le cercle unité C centré à l'origine. Donc le pôle -2-\sqrt{3} ne se trouve pas à l'intérieur de C : êtes-vous d'accord?

Posté par
Mathes1re : Intégral par le Théorème de Résidus 1 31-10-23 à 21:11

Bonjour
C'est parce que entre 0 et 1 le cercle de rayon 1 maximum
Et la méthode usuelle qui donne 0?
Merci

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 31-10-23 à 21:24

quelles sont les bornes de la méthode usuelle ?

Posté par
Mathes1re : Intégral par le Théorème de Résidus 1 31-10-23 à 21:27

Bonsoir
Entre 0 et 2π ou ça change
Je me doute ici
S'il vous plaît est ce que cette justification est juste

Citation :
C'est parce que entre 0 et 1 le cercle de rayon 1 maximum

Merci

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 31-10-23 à 21:31

dans la méthode usuelle ( dont vous donnez le résultat qui est exacte il n'y a pas de borne définie) quand vous faites le changement de variable t= tg(\dfrac{\theta}{2}) les nouvelles bornes d'intégrations sont lesquelles?
On ne peut pas trouver la même car on intègre sur intervalle différent.

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 31-10-23 à 21:33

On ne peut pas trouver la même chose car on intègre sur intervalle différent de la méthode que vous appelez usuelle.

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 31-10-23 à 21:34

Finalement combien trouvez-vous pour J1?

Posté par
Mathes1re : Intégral par le Théorème de Résidus 1 31-10-23 à 21:40

Bonjour

Citation :
C'est parce que entre 0 et 1 le cercle de rayon 1 maximum

Oui c'est totalement juste
Finalement J1=\dfrac{2\sqrt 3}{3}\pi
Merci

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 31-10-23 à 21:42

vous dites C'est parce que entre 0 et 1 le cercle de rayon 1 maximum .

C'est mal dit mais je pense que vous avez compris. Les pôles à prendre en compte doivent se trouver à l'intérieur du cercle de rayon 1 dont le centre est (0,0).

Posté par
phyelec78re : Intégral par le Théorème de Résidus 1 31-10-23 à 22:05

oui, je trouve le même résultat que vous pour J1.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !