Bonsoir Denis79

Oui c'est possible mais avec un calcul monstrueux de primitives

alors que le passage en coordonnées polaires (comme tu l'as vu) donne le résultat immédiatement !

On a si on note ,

et en utilisant Fubini

ce qui donne par une première primitivation


puis par une seconde

c'est à dire (finalement ) _{sauf erreur de ma part bien entendu}

Ah oui effectivement , compliqué les primitives... - Bravo et merci

Nous trouvons effectivement le même résultat.

Juste une question qd tu utilises Fubini, je ne comprends pas d'où vient le le facteur 2 devant la racine ? peux tu m'éclairer svp ?

Moi, ce que je ne comprends pas, c'est l'énoncé. Que fais tu de z ? Et c'est qui, cette fonction f ?

Denis79 Au début on avait plutôt

puis par parité (pour fixé) de la fonction, on a, .


Ulmiere le volume à calculer n'est autre que le volume sous le graphe de la fonction continue et positive , ,


c'est pareil au cas d'une fonction réelle à une variable qui est continue et positive :


où _{sauf erreur de ma part bien entendu}

@Ulmiere, Bonjour

J'écris sous le couvert de verification  En fait la fonction f(x,y) est une fonction à deux variable. La coordonnées en z est justement la fonction z=. Et l'on calcule le volume sous cette fonction sur le domaine D, délimité par les autres conditions données sur le volume. Si j'ai bien compris la description du volume, l'aire D est un demi-cercle de rayon 1 entre 0 et . Quelqu'un peut-il confirmer svp ?

Oui Denis79 je confirme

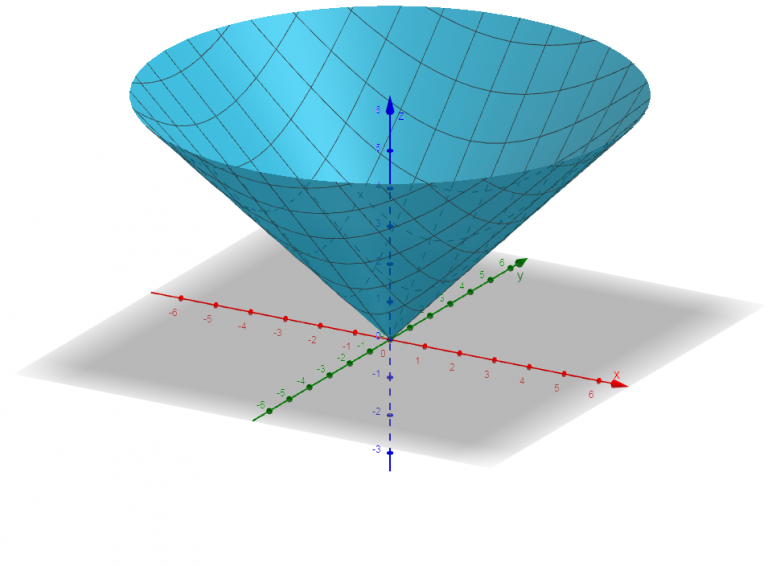
On pouvait aussi remarquer que la surface est un demi-cône de révolution de sommet

et que le volume à calculer est la moitié du volume de la zone inférieure coincée entre le cylindre

et la surface cônique ce qui donne _{sauf erreur de ma part bien entendu}

Merci, Ah oui effectivement c'est une autre méthode

C'est un plaisir Denis79