Inscription / Connexion Nouveau Sujet
Intégration et suite avec utilisation de la dérivée seconde
Bonjour ! je travaille des exercices pour la rentrée mais je bloque carrément sur celui ci...
J'espère que vous pourriez m'aider 
Voici mon exercice
Pour tout n ∈ N, on considère la fonction fn définie par
∀t ∈ R, fn(t) = (t - t2 )n
et l'intégrale In donnée par
In = (π 2n+1 n!)
fn(t) sin(πt) dt
1. a) Calculer I0 et I1
b) Soit n ∈ N \ {0; 1}.
Démontrer que ∀t ∈ R,
f′′ n (t) = −2n(2n − 1)fn-1(t) + n(n − 1)fn−2(t)
et en déduire que
In = 2(2n − 1)In-1 − π 2 In-2
J'ai réussi à trouver I0 et I1 avec des IPP
Mais pour la derivee je ne trouve pas la meme chose :
et je n'arrive pas du tout à faire l'expression de In
Merci pour votre aide !
lqpdcr 
C'est assez difficile d'écrire des maths sur ordinateur, voici donc ce que j'ai su faire pour le moment 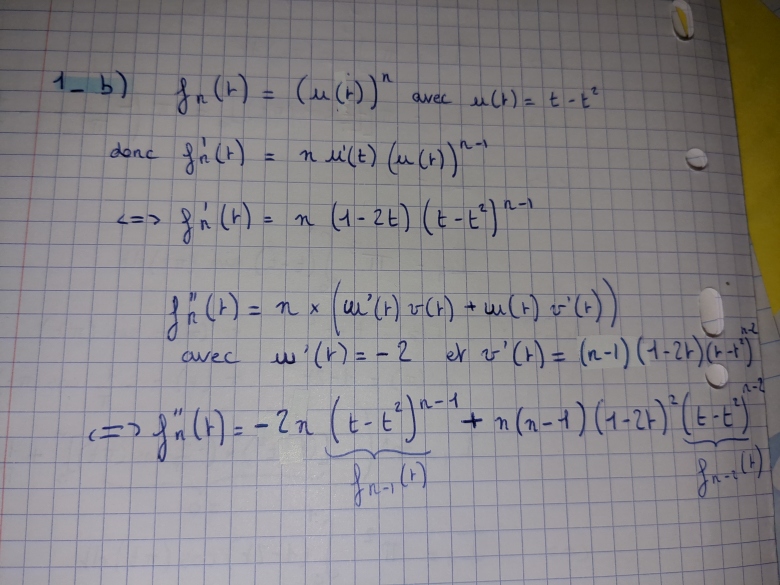
Merci
Ok merci beaucoup pour la piste je vais essayer de travailler là dessus, je reviens ici si je bloque encore !
Merci c'est bon !!!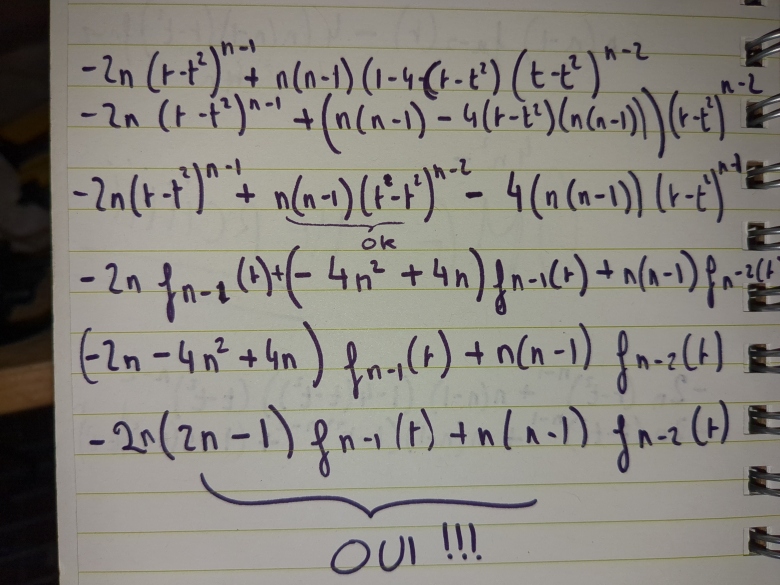
Mais du coup je n'arrive pas non plus la deuxième partie de la question 😬 :
et en déduire que In = 2(2n − 1)In-1 − π 2 In-2
Bonsoir lqpdcr 
Pour alléger les calculs notons
on a alors
.
Une double intégration par parties donne
...

Bonjour à tous les deux
lqpdcr le règlement ne t'autorise pas à poster ce type d'image. Merci de ne plus le faire, nous avons plein d'aides d'écriture sur le site.
Aide toi de l'assistant Ltx éventuellement ( icône Ltx avec les 2 petits points rouges dessous) Fais quelques essais tu vas voir on prend très vite le coup.
Ah désolé je pensais que c'était possible une fois qu'on avait écrit l'énoncé de l'exo
Merci elhor_abdelali
je vais essayer avec cette piste 



 analyse en post-bac
analyse en post-bac