Inscription / Connexion Nouveau Sujet
Intégration par parties
Bonsoir à tous,
J'ai un peu du mal a résoudre ce problème :
Soit In= sinnx.dx de o a pie/2 pour tout n € R
sinnx.dx de o a pie/2 pour tout n € R
1. Calculer I0 et I1
2.A l'aide d'une integration par parties, démontrer que In=(n-1)/n * In-2 pour totu n>= 2
+ dautres kestions mais la deja je bloque pour la deuxieme question .
j'ai trouvé tout I0=1 et I1= -cospie/2 +cos0 =1
pour la deuxieme j'ai tenter deja de faire une ipp de In mais j'obtient des lignes de calculs faramineuses dans leskelles je me perd et ou je ne trouve malheureusement aucune signification
j'ai egalement essyant de partir de (n-1)/n * In-2 de retomber sur In en ipp In-2 mais idem je m'enfonce
j'ai essayer un tas de maniere verifié x fois mes calculs je ne tombe pas sur le resultat attendu
Quelqu'un aurait-il un tuyau pour moi ?
les integrals de Walis, un grand classique ^^
pour I1 je suis d'accord avec toi, pour Io revoi ton calcule ^^ (on trouve Pi/2)
pour l'ipp tu par de In, tu prend u'=sin v=sin^(n-1)
tu va te retrouver avec un cos² qu'il faudrat remplacer par 1-sin² et t'aura une expression avec des In et des In-2
a partir de la tu isole les In et tu trouve exactement ce qu'il faut.
apres je suppose qu'on te demande de montre que In est decroissante, sa tu le fais avec les expression integrales et a priori a partir de la tu doit oublier ces expression et tous faire avec la relation de recurence ^^ (enfin en general c'est comme sa)
okey , déja merci d'avoir répondu si rapidement c'est très sympa
alors allons-y
u'= sinx
u = -cosx
v= sinn-1 x
v'= (n-1)cosx.sin(n-2)x
In= [uv] - v'.u
v'.u
= [-cosx.sinn-1 x ] -  -(n-1)cos2x.sin(n-2)x
-(n-1)cos2x.sin(n-2)x
= [-cosx.sinn-1 x ] -  -(n-1)(1-sin2x).sin(n-2)x
-(n-1)(1-sin2x).sin(n-2)x
= [-cosx.sinn-1 x ] - -(n-1) (1-sin2x).sin(n-2)x
(1-sin2x).sin(n-2)x
= [-cosx.sinn-1 x ] + (n-1) (  sin(n-2)x -
sin(n-2)x -  sinnx )
sinnx )
mais je commence à tourner en rond :s j'avais essayé ca (mais j'avais pas pensé au cos^2 = 1-sin^2  )
)
Voici un plus qui va surement t'aider à faire la suite de tes questions 
Avec cette relation , on peut calculer I2p et I2p+1:
Par récurrence on a donc :
Donc en multipliant par les termes paires 2p(2p-2)...2 au numérateur et au dénominateur, on a:
donc en factorisant par 2² au dénominateur on a donc:
De meme pout I2p+1 et on trouves:
j'ai juste un petit prob .. c'es( sur que la primitive entre 0 et pi/2 vaut o ??
en tout cas thanks à tous les deux 
On peut montrer que la suite Un définie par Un=nInIn+1 est constante.
On a:
Or
donc
donc Un est constante 
c'est dingue ! exactement la suite de mes question .. t'es dans ma classe ou bien c'est un exercice type ?
En fait c'est un sujet très classique et je l'ai fait l'année dernière en prépa 
Pour en revenir à Un, je me suis trompé dans certain signe (faute de frappe )
On a Un=nInIn-1
et Un+1=(n+1)In+1In=nInIn-1=Un 
On a vu qu'elle était constante
donc pour tout n de N*, Un=U1 (par exemple)
Or U1=I0=pi/2
donc pour tout n de N*,
On peut aussi montrer que In ~ In+1 quand n->+oo.
On a plusieurs méthodes.
En se servant de la formule établie précédemment, on a:
d'où
d'où In+1 ~ In-1 en n->+oo
De plus pour tout n de N* et pour tout x de [0,pi/2], on a:
donc
(In est donc decroissante)
On en déduit donc que In+1 ~ In quand n-> +oo
Finalement on peut aussi montrer que In ~ .
On a en utilisant les formules établies de I2p et I2p+1 :
Comme I2p+1 ~ I2p et I2p > 0, on en déduit que :
I2p ~
puis
I2p+1 ~
donc finalement :
Voila sauf erreur de ma part
Joelz
sauf erreur, cela permet d'établir la formule de Stirling, non?
Neo
Oui je crois 
Stirling et Wallis sont très copains 
Finalement on peut aussi montrer que In ~ .
On a en utilisant les formules établies de I2p et I2p+1 :
Comme I2p+1 ~ I2p et I2p > 0, on en déduit que :
I2p ~
puis
I2p+1 ~
donc finalement :
Voila sauf erreur de ma part
Joelz
salut zeyniba si tu veux aller plus loin, par exemple; si tu veux trouver I2p et I2p+1 (plus précisément les valeur de In selon la parité de n), il suffit de faire une ittération de la formule que tu vien d'obtenir:
si n est paire:
.....
I3=(2/3)I1
I5=(4/5)I3
...
...
...
I2p+1=(2p/2p+1)I2p+1 d'ou I2p+1=2.4.6......2p .
1.3.5.7......(2p+1)
De maniere analogue éssais de trouver I2p?
"sauf erreur, cela permet d'établir la formule de Stirling, non?"
plus ou moins
stirling ce demontre en deux etape :
d'abord on montre que n! ~ k*sqrt(n)*(n/e)^n
(resultat obtenu par Moivre)
puis on montre (en etudiant utilisant cette equivalent par exemple) que k=sqrt(2*Pi)
J'aiun petit pb avec la formule de conjecture de I2p et I2p+1
I2= (2-1)/2 Io = (1/2)Io = (1/2) (pi/2)
avec la formule I2p on a p=1
en l'appliquant on a : (2x1)! / (22x1) (2!)2 x Io = 2/(4x4)Io =1/8 Io I2= 1/2 Io
I2= 1/2 Io
Ou est le probleme ? 

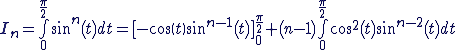
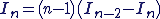





 analyse en post-bac
analyse en post-bac