Inscription / Connexion Nouveau Sujet
Inverse de la somme et somme des inverses !
Bonjour  !
!
Demain (comme je l'ai déjà dit dans un prècedent post) j'ai un contôle sur les fonction de réference et donc je m'entraine , je m'entraine , je m'entraine... et je fais (tout du moins j'essaie de faire) les exercices d'approfondissement que je trouve.
J'ai bossé une majeure partie de la journée , mais plus j'avance plus les exos se compliquent.
Dont celui-ci.. Je pense que j'aurais un exercice de ce genre demain , donc j'aimerais le faire (avec l'aide de votre part).
Si certaine personne veulent bien m'aider ...merci d'avance.
Voici l'énoncé et ci-joint un petit schéma que j'ai fait pour vous donnez une idée.
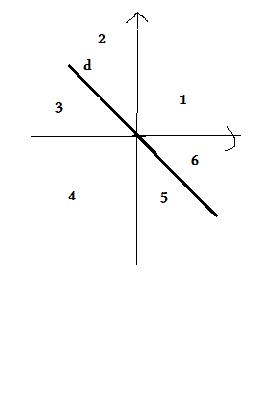
a) d est la droite qui représente la fonction x |--> -x dans un repère.
Les points qui n'appartiennent ni à d, ni aux axes des coordonnées se répartissent en six zones numérotées de 1 à 6 sur la figure ci-contre.
On choisit un point M(x;y) tel que : x different de 0 ; y different de 0 et y different de -x.
Indiquer suivant le numéro de la zone dans laquelle M se trouve, le signe nu nombre xy(x+y).
b) Démontrer que, quels que soient les réels x et y :
(x+y/2)² + 3y²/4 = x²+y²+xy.
c) Comparer , pour x différent de 0 ; y different de0 et x+y different de 0 , l'inverse de la somme de x et y avec la somme des inversses de x et y.
Les conclusions seront données suivant la position de M(x;y) dans l'une des six zones définies à la question a).
Bonjour
Commence par caractériser par des inégalités chaque zone. Par exemple (x,y) est dans 6 si et seulement si x 0, x+y
0, x+y 0 et y
0 et y 0
0
Dans le repere :
-(x,y) est dans 2 si et seulement si x>0, x+y >0 et y <0
- ....
Je ne comprend pas ??
Bonjour à tous  .
.
Voici un début d'exercice que je n'arrive pas à saisir.(Ci-joint , je vous ai fait un petit croquis ..)
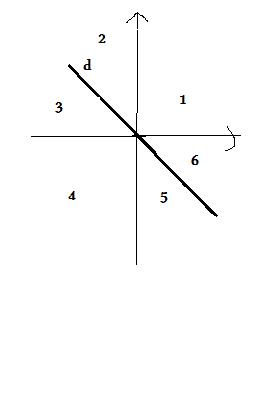
a) d est la droite qui représente la fonction x |--> -x dans un repère.
Les points qui n'appartiennent ni à d, ni aux axes des coordonnées se répartissent en six zones numérotées de 1 à 6 sur la figure ci-contre.
On choisit un point M(x;y) tel que : x  0 ; y
0 ; y  0 et y
0 et y  -x .
-x .
Indiquer, suivant le numéro de la zone dans laquelle M se trouve, le signe du nombre xy(x + y).
Pouvez vous m'aider , je bloque.
Merci d'avance.
Edit Coll : image supprimée
*** message déplacé ***
Bonjour,
N'oublie pas que le multi-post est interdit dans ce forum :
Relis ceci 
![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
Ainsi que les réponses aux questions Q02 et Q03 de la FAQ 
![]() [lien]
[lien]
Il est très facile de retrouver ses messages : 
![]() [lien]
[lien]
Clique sur les maisons, ce sont des liens !

Très bien. Je ferais attention la prochaine fois.
Pour l'exercice , je dois trouvé où se situe M , à l'espace 2 ; 3 ; 4 ; 5 ; 6 ; ou 1 ... mais je ne comprend pas comment je dois proceder ??
Pourriez vous m'éclairer?
J'ignore complétement comment faire ... car je ne sais pas si faut étudier chaque zone , pr trouver par la suite M... ou si M est ds chaque zone... et quelle calcul faire ?!
Bonjour.
J'ai finalement réussi à avancer , pouvez vous me corriger ?
Enoncé:
a) d est la droite qui représente la fonction x |--> -x dans un repère.
Les points qui n'appartiennent ni à d, ni aux axes des coordonnées se répartissent en six zones numérotées de 1 à 6 sur la figure ci-contre.
On choisit un point M(x;y) tel que : x different de 0 ; y different de 0 et y different de -x.
Indiquer suivant le numéro de la zone dans laquelle M se trouve, le signe nu nombre xy(x+y).
b) Démontrer que, quels que soient les réels x et y :
(x+y/2)² + 3y²/4 = x²+y²+xy.
c) Comparer , pour x différent de 0 ; y different de0 et x+y different de 0 , l'inverse de la somme de x et y avec la somme des inversses de x et y.
Les conclusions seront données suivant la position de M(x;y) dans l'une des six zones définies à la question a).
Pouvez vous me dire si ce que j'ai trouvé est correct ? :
a) Pour la zone 1 les coordonnées du point M (x;y) sont possitif.
Pour la zone 2, x = negatif y= possitif
Pour la zone 3, x=negatif et y= posotif
Pour la zone 4, x=negatif et y =negatif
Pour la zone 5, x=possitif et y=negatif
Pour la zone 6, x=positif et y=negatif
Donc . ?! je ne sais pas trop enfaite pr cette question ...
b)(x+y/2)² + 3y²/4
= x² + 2x x (y/2)² + (y/2)² + 3y²/4
= x² + 2xy/2 + y²/4 + 3y²/4
= x² + xy + 4y²/4
= x² + xy + y²
Est-ce bon?
c) Est-ce pareil que pr la a) ??
Merci à l'avance pour vos réponses et votre aide.
A très vite.
*** message déplacé ***
bonjour
1) ta réponse est exacte
2) xy est négatif
x+y sera >0 puisque x<0
donc xy/(x+y) sera <0
3) xy est négatif
x+y sera <0 car IxI>IyI
donc xy/(x+y)>0
4) x<0
y<0
donc xy>0
x+y<0
le rapport est donc <0
tu sauras bien conlure pour 5) et 6)
ton calcul de b) est exact
c)
1/x+1/y=(x+y)/xy
tu dois donc comparer
1/(x+y) et (x+y)/xy
partons de l'hypothèse
1/(x+y)>(x+y)/xy
et regardons en fonction des zones de la question 1) si celle ci est vérifiée
xy>(x+y)²
0>x²+xy+y²
or si tu te reportes à ce que tu as calculé en question b) tu dois pouvoir conclure sans difficultés
salut
*** message déplacé ***