Inscription / Connexion Nouveau Sujet
Inverse de la somme et somme des inverses
Bonjours,
j'
ai un exercice à faire et je n'arrive pas à résoudre la dernière question.
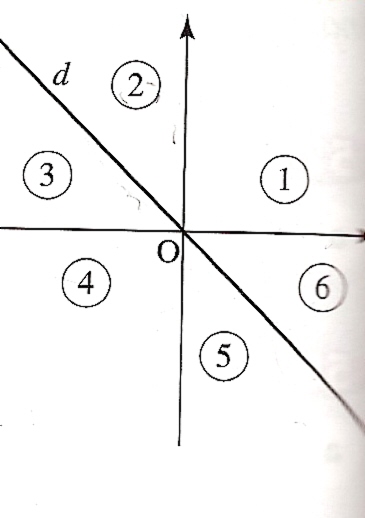
d est la droite qui représente la fonction x→ -x dans un repère. Les points qui n'appartiennent ni à d, ni aux axes de coordonnées se répartissent en six zones numérotées de 1 à 6 (voir la figure ci-jointe). On choisit un point M(x;y) tel que :
x≠0, y≠0 et y≠0.
c) Comparer, pour x≠0, y≠0 et x+y≠0, l'inverse de la somme de x et y avec la somme des inverses de x et y (on pourra étudier le signe de leur différence).
Les conclusions seront données suivant la position de M(x;y) dans l'une des six zones définies à la question a).
Merci de bien vouloir m'aider.
Bien sûr que non ! n'est facteur ni du numérateur, ni du dénominateur !
Mais ce qui t'intéresse, c'est le signe de cette fraction, non ? Alors réfléchis : montre que le numérateur est positif !
Comment faut il faire pour trouver que le numérateur est positif car j'ai cherché et je ne trouve pas
x²+y²+xy est compris entre x²+y²+2xy et x²+y²-2xy (on ne sait pas lequel des deux est le plus petit car cela dépend du signe de x et de y, mais en tous cas x²+xy+y² est bien compris entre ces deux nombres. Or x²+2xy+y²=(x+y)² et x²-2xy+y²=(x-y)². Donc, x²+xy+y², compris entre deux carrés, c'est à dire entre deux nombres positifs, est forcément positif !
Une autre méthode est de connaître l'identité remarquable : . Donc :
Or, on sait que la fonction est croissante sur
. Par conséquent
est toujours du même signe que
et leur rapport,
est donc positif !
Annuler
connectez vous