Inscription / Connexion Nouveau Sujet
L'ensemble H est une hyperbole?
Bonjour,
Je voudrais savoir comment on fait pour prouver que (tous les coeff sont réels et a, c et f sont non-nuls) est une hyperbole dans un repère orthonormé
.
Par exemple (celle qui m'importe):
Pour info: cet hyperbole a pour foyers F(-2,-4) et F'(8,1). L'image attaché représente ce que je trouve quand je la trace sur GeoGebra:
salut
déjà dans l'exemple présent simplifier les coefficients ....
ainsi les coefficients de x2 et y2 sont de la forme (a - b)(a + b) ...
ensuite faire disparaitre le coefficient de xy par un bon changement de variable ....
Bonjour,
Il suffit de calculer le discriminant de l'équation qui correspond à b²-4ac (qui est indépendant du repère orthonormal direct dans lequel on se place). Si le discriminant est strictement positif, alors la conique est de type hyperbole.
Dans ton exemple, on a b²-4ac=147793.8921 (d'après Maple).
>Carpediem: Le coefficient de x² est et celui de y²
.
faire disparaitre le coefficient de xy par un bon changement de variable
>Kaname: Effectivement je trouve le même résultat. Mais là je me demande: pourquoi cette condition est suffisante pour que
ouais de toute façon ça reste un peu théorique ici vu tes coefficients .... et même en les simplifiant tous ... enfin faudrait voir ....
donc déjà réduire tous les coefficients puis simplifier ....
peut-être serait-il intéressant de savoir d'où provient cette équation ?
tj intéressant d'avoir une formule magique qui donne la réponse ... pour savoir ... mais quand on apprend le pb est presque tj de savoir pourquoi ....
le changement de repère ::
x = au + bv + c
y = du + ev + f
permet d'obtenir la forme canonique (les lettres de mon système ne sont pas ceux de l'équation ....)
mais le trouver en regardant simplement ici ....
peut-être un logiciel de calcul formel le fait-il ....
@Manga2 : si tu es parti des coordonnées des deux foyers et d'un point de l'hyperbole pour établir ton équation, je t'ai expliqué ici 
Hyperbole définie par deux foyers et un point d'elle comment trouver les a et b (ou et
, c'est selon) de l'équation réduite. Quant à avoir un repère orthonormé où l'équation est réduite, c'est simple : le centre (milieu des foyers) est l'origine, et la droite des foyers te donne le premier axe.
carpediem et GaBuZoMeu: merci! Mais je ne dois pas changer de repère.
>carpediem: c'est quoi la forme conique? Je ne suis qu'en première (Lycée) et je passe au terminal.
>GaBuZoMeu: Cette hyperbole a pour foyers et
et passe par le point
.
Donc si je veux écrire son équation sous la forme j'ai donc comme tu l'as cité:
et
.
Je procède au calcule et je trouve: et
Donc
Je trace sur Maple et je trouve: 
C'est différent, ou me suis-je trompé dans les calcules?
la forme canonique !! ben c'est ce que tu obtiens après réduction ... tout comme ta dernière écriture ... manque peut-être un carré pour y ....
Je vois. Mais je n'y arrive pas. Il faut factoriser les x et y grâce aux identités remarquables, mais que faire de xy?
L'équation réduite d'une conique, c'est une équation dans un autre repère orthonormé que celui de départ. Ou, si l'on veut garder le repère, ça revient à déplacer la conique (de manière isométrique, sans la déformer).
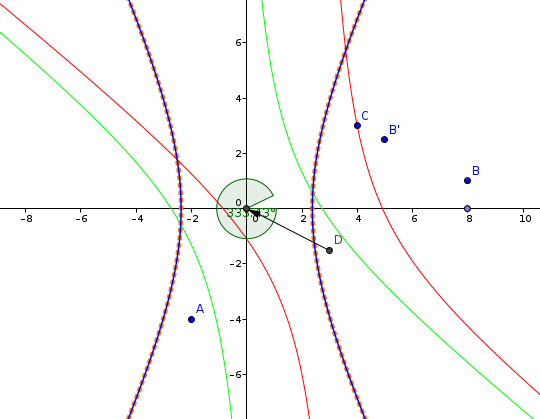
C'est illustré sur le dessin qui suit. En rouge, l'hyperbole qui t'es donnée. En vert, l'hyperbole translatée de façon à ce que son centre coïncide avec l'origine. En vert, on a fait tourner autour de l'origine de façon à ce que l'axe des foyers coïncide avec l'axe des abscisses.
Et en orange pointillé, l'hyperbole donnée par l'équation réduite que tu as trouvée : ça coïncide bien avec l'hyperbole bleue !
Merci pour ton explication. Moi, je cherche les points d'intersection de deux hyperboles dans le plan qui n'ont pas le même sommet. Je pense que je devrai donc translater les deux par (S est le sommet de la première hyperbole) et appliquer la même rotation pour les deux. Je n'aurais plus qu'à faire de nouveaux calcules. Une fois les points d'intersection trouvés, je vais ajouter à leurs abscisses celui de S et de même pour leurs ordonnés. Et voilà les points trouvés.
STP, Kaname a dit:
Il suffit de calculer le discriminant de l'équation qui correspond à b²-4ac. Si le discriminant est strictement positif, alors la conique est de type hyperbole.
Parce que ça veut dire que la conique a deux points à l'infini.
Autrement dit, que la partie du second degré de l'équation factorise en (sx+ty)(ux+vy), chacun des facteurs donnant la direction d'une asymptote.
C'est simplement que factorise en un produit
(tous les coefficients sont réels) si et seulement si
.
factorise en un produit
si et seulement si
Les directions des asymptotes de l'hyperbole sont données par les facteurs et
.
Supposons que ni ni
ne sont nuls.
Si l'équation de l'hyperbole est , que peut-on voir sur la limite de
quand
tend vers l'infini ? (indication : diviser cette équation par
).
On a
Donc:
Donc:
Dans notre cours de première sur les branches infinies des fonctions, soit une fonction numérique avec un domaine de définition qui s'étend jusqu'à l'infini. Ce qui suit est valable pour +
et -.
Si alors
, la représentation graphique de
, admet une branche parabolique en +
dirigée vers l'axe des ordonnés.
C'est quand que
admet une asymptote (sauf dans un cas bien précis non étudié).
De cela, puisque , alors
admet deux branches hyperboliques dirigées vers l'axe des ordonnés en
et non pas des asymptotes, ou me suis-je trompé dans mes calcules?
Oui, tu t'es trompé. Si j'ai mis la partie du second degré sous forme factorisée, c'est bien pour qu'elle reste comme ça.
Tu fais tendre vers l'infini, et tu regardes les limites possibles pour
.
On a donc:
Mais après je ne sais plus quoi faire.
J'ai essayé quelque chose, mais je n'en suis pas sûr.
Pour dépasser les calcules banales du delta et autre, j'ai utilisé Maple, en posant sans remplacer les autres x, ce qui donne:
solve(,z) signifie résoudre l'équation
d'inconnu z.
limit(f(x),x=infinity) signifie
Résultats sur Maple:ici 
et ici 
En supposant que le contenu de la racine est positif et que les limites ne sont pas nulles, donc admet effectivement des asymptotes.
Tu t'emmêles les pinceaux.
Si est la limite de
quand
tend vers l'infini sur une branche infinie de l'hyperbole, on obtient à la limite dans
:
Donc...
Mais qui nous dit que la limite en infini de est fini? Mais bon...
On a:
Donc ou
En fait,
Donc
S'il y a une branche d'hyperbole le long de laquelle tend vers l'infini, alors
ne tend pas vers l'infini le long de cette branche.
Selon toi ne serait pas une hyperbole puisque cette équation ne contient ni
ni
?
C'est une hyperbole. Mais si alors il ne s'agit pas d'une asymptote mais d'une branche parabolique dirigée vers l'axe des abscisses.
Je viens tout juste de trouver un PDF:
La définition 5 (page 19) dit: Le discriminant de la courbe d'équation dans le repère
est le nombre
La définition 6 (page 20) dit: [...] Une conique de discriminant strictement négatif est une conique du genre hyperbole.
Effectivement le discriminent de est strictement négatif.
Piocher des PDF sur le net sans trop comprendre ce qu'il y a dedans ne me semble pas une manière de travailler très profitable.
Là, tu racontes un peu n'importe quoi. Une hyperbole a toujours deux asymptotes, éventuellement une asymptote horizontale () ou une asymptote verticale
)
L'hyperbole a une asymptote horizontale et une asymptote verticale, bien sûr. Et tu remarqueras que la factorisation de la partie de second degré de l'équation
donne bien les directions des deux asymptotes.
Quand au discriminant, c'est bien ce qu'on (Kaname et moi) te dit depuis le début !
Ah désolé, vous m'avez dit b²-4ac et sur le PDF c'était b²-ac mais il ne s'agissait pas en fait du même b. Désolé^^
Piocher des PDF sur le net sans trop comprendre ce qu'il y a dedans ne me semble pas une manière de travailler très profitable.
En fait, je lis ces PDF page par page, crois-moi. Mais j'avoue que je ne fournis pas mon maximum d'effort pour tout comprendre. En fait, avant même que je ne poste une question concernant les hyperboles, si j'avais vraiment voulu TOUT comprendre, et surtout que les PDF contiennent des choses non-étudié, j'aurais pris entre 2 et 4 semaines pour tout gober, mais je n'ai pas voulu le faire, parce que la raison avant tout qui m'a poussé à étudier les hyperboles est un problème concernant les intersections des hyperboles. Le problème lui-même est difficile. Mais je ne pensais pas que ça sera si compliqué que ça, de le traiter analytiquement (à mon niveau, en géométrie analytique, on a étudié les points, les droites, les vecteurs, le produit scalaire et le cercle. En géo-3D, même chose (sauf le cercle, mais on l'a parfois définie par l'intesection d'un plan donné avec une sphère donné: Cercle de centre.. et de rayon..) et en plus de cela le produit vectoriel)). Ensuite, je dois couvrir le maximum de chapitres de terminale pour fournir du temps pendant l'année scolaire (et par couvrir, non seulement comprendre le cours et faire les exercices classiques, mais aussi les exercices les plus dur et des problèmes extras proposés dans le manuel. Un example concernant la continuité, simple certes, mais difficile pour un élève en première, et c'est encore rien comparé aux autre problèmes.
Distance d'un point à l'ensemble Z ). Depuis 17 juillet jusqu'au 12 Août, je n'ai couvert que deux chapitres, la continuité et les suites (et je n'ai pas encore commencé problème concernant les suites). Deux leçons hyper faciles! Et de plus, on avait acquis quelques notions concernant la continuité en première (notre prof nous fais signe parfois de chose qu'on a pas encore étudié) donc ce n'était pas tout à fait nouveau pour moi. Et dans ma branche Sc.Maths en terminal (je ne suis pas en France), on n'a pas de géo analytique du tout (sauf celle utilisant les nombres complexes). Et quand même, ça fait une semaine que je travaille sur les hyperboles, une semaine de "perdue". J'ai appris grâce à toi, et à tous ces gens formidables qui ont perdu leur temps précieux pour m'aider, des choses interessantes, et j'en suis fier. Je ne suis pas du genre à travailler les maths pour un certain examen, j'aime les maths pour ce qu'ils sont, mais j'ai des priorités: le programme riche des maths du terminal et (comme je l'ai fait en maths), il me reste à réviser le programme de physique de première. D'ailleurs, depuis que je suis enfant, en été, je fais une dizaine ou une vingtaine d'exercices de maths. Cet été, c'est le premier où j'attaque l'année prochaine.
Bref (oula j'ai trop écrit, je n'ai même pas vu cque j'écrivais), je pense que je devrais abandonner (pour le moment!) et laisser cela à l'été prochain, à ce moment là, j'ai les 2 semaines à offrir pour tout comprendre. J'ai sauvegardé ces pages pour garder les informations.
Encore merci à toi et à tout ceux qui m'ont aidé!
Je te félicite pour tes efforts. Mais les documents qu'on peut trouver sur le web ne sont pas forcément les meilleurs du point de vue pédagogique ou les plus adaptés à tes connaissances actuelles.
Quel était ton problème d'intersection d'hyperboles ?
^^ Secret :p
Autre les PDF, que faire? Engager un prof particulier? Effectivement c'est bien meilleur qu'étudier seul. C'est coûteux, certes, mais la science n'a pas de prix. Sauf que je suis en voyage dans un village (pas de profs sup là-bas) et aussi bien que j'étudie, je profite de la plage et des vacances, engager un prof c'est s'engager avec lui en déterminant des heures pour les séances, sauf que moi, je n'étudie que lorsque j'en ai envie. Si à un moment de la journée j'en ai pas envie, alors ça ne sera pas pratique. Quant à mon père qui est professeur universitaire, le jour où il a vu le PDF sur les coniques, il a lu des choses nouvelles pour lui. La définition par l'excentricité, il n'en a jamais entendu parler. C'est normal: il fait de l'analyse numérique (surtout les matrices), pas de géométrie. Mais puisque c'st analytique il peut tout m'expliquer, mais il a aussi son propre travail à faire. Mon père, à chaque fois que je ne comprends pas quelque chose, il me consacre son temps, et cet été même, quand il me voit lire un cours de terminal, il intervient pour voir le cour des choses, et si j'ai bien compris (en livre scolaires, contrairement aux PDF, ça suit un problème donc une leçon ne demande de préquis autre que ceux déjà apprises, et après chaque partie du cours, des exercices d'application), même s'il a ses propres articles à rédiger. Et là il s'agit d'un cours qui demande des préquis non étudiés, ça sera trop demandé, même s'il voudra me consacrer des semaines avec plaisir (des semaines que moi-même je ne suis pas prêt à gaspillé comme expliqué précédemment), ça sera un fardeau pour lui.
Maintenant que j'écrivais, Youtube m'est venue à l'esprit. Mais bon, s'il y a de bonnes videos, pour tout maitriser ça me demandra quand même 1 semaine entière.
Annuler
connectez vous
géométrie en post-bac