Bonsoir,

C'est facile, surtout si on ne te demande pas de justification 'rigoureuse' :

Voici la représentation graphique de la fonction carré (enfin, un morceau). On voir sur la figure que lorsque les abscisses (x) est entre -1 et 2 (en rouge), les ordonnées des points de la courbe (f(x), ici x²) se trouvent entre 0 et 4. Donc pour -1 ≤ x ≤ 2, on a l'encadrement 0 ≤ x² ≤ 4.



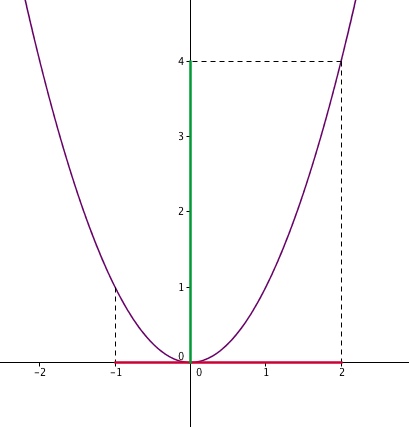
Tu vois ?

Tu fais pareil pour tous tes intervalles, c'est pas très passionnant une fois qu'on a compris, mais ça va vite .

mes réponses sont ils juste pour:
a) 4 < X² < 16
b) X² e[-9;0]
c) -4 < X² < 4
d) X² e[-16;0]
e) 0 < X² < 16
f) X² e]-64;25[

a) et e) sont justes. Revois les autres...

Un carré n'est jamais négatif : tu le sais, et ça se voit sur la figure (aucune ordonnée f(x) n'est négative, la courbe reste au-dessus de l'axe des abscisses).

mes réponses sont ils juste pour:

b) X² e[9;0]
c) 4 < X² < 4
d) X² e[16;0]
f) X² e]64;25[

Là tu as juste changé tous tes - en + ...
Réfléchis deux minutes, est-ce que [9;0] est un intervalle ? sachant que 9 est plus grand que 0, il n'y a pas beaucoup de nombres là-dedans...
De même, il n'y a aucun nombre qui soit à la fois > et < à 4...
Bref, tes intervalles n'ont pas beaucoup de sens...

Je te re-montre sur un autre : -3 ≤ x ≤ -1 :



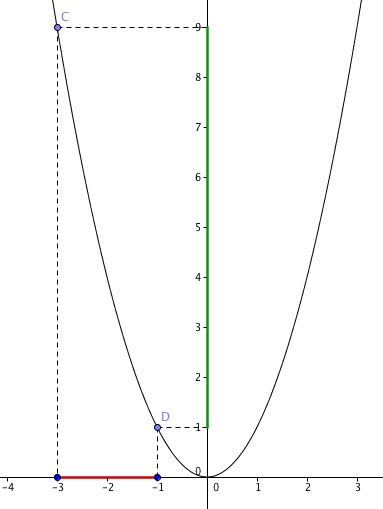
Pour le morceau de courbe qui correspond aux abscisses entre -3 et 1 (le morceau entre les points C et D, donc), quelles sont les valeurs que prend f(x) (les valeurs prises en ordonnée) ?
--> réponse : les ordonnées correspondantes forment l'intervalle [1,9]