Inscription / Connexion Nouveau Sujet
la parabole
bonjour!
voilà, j'ai un exo de maths et je ne sais pas trop comment m'y prendre.
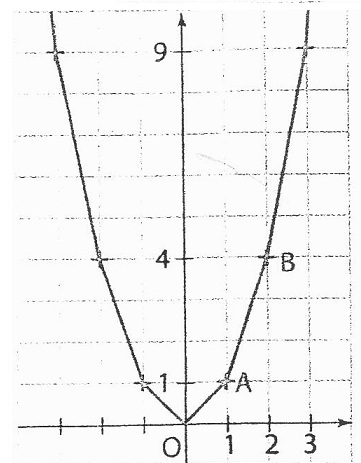
Un élève a placé quelques points de la parabole P représentant la fonction carré. Ensuite il a rejoint ces points avec la règle.
1. On se propose de démontrer que la parabole P ne contient aucun segment de droite. u et v désignent deux réels tels que 0 < u < v.
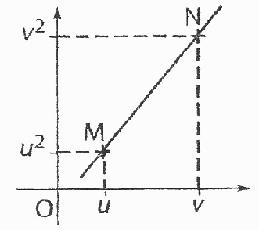
M(u;u²) et N(v;v²) sont deux points de la parabole P.
a)La droite (MN) représente une fonction affine f(x)=ax+b.
Expliquer pourquoi a = u + v.
Vérifier alors que b = u²-(u+v)u.
b)On note x un réel de l'intervalle ]u;v[.
P(x;x²) est un point de la parabole P et Q(x;yQ) est un point du segment [MN].
Vérifier que yQ - x² = (x-u)(v-x).
En déduire le signe de yQ - x².
Si vous pouviez m'aider à comprendre...
merci d'avance.
Bonjour,
le coeff "a" de la droite (MN) est donné par :
a=(yN-yM)/xN-xM)=(v²-u²)/(v-u)=[(v+u)(v-u)]/(v-u)=v+u (ou : u+v)
On peut simplifier ^par (v-u) car (v-u) 0
0
Cette droite a donc une équa de la forme :
y=(u+v)x+b
Elle passe par le point (u;u²) donc on peut écrire :
u²=(u+v)*u+b qui donne b=u²-(u+v)u
b)
yQ=(u+v)x+u²-(u+v)u
yQ=ux+vx+u²-u²-uv
yQ=ux+vx-uv
yQ-yP=ux+vx-uv-x²
Vérifier que yQ - x² = (x-u)(v-x).
On développe (x-u)(v-x) et on retrouve : xv-x²-uv+ux soit : ux+vx-uv-x²
Donc :
yQ - x² = (x-u)(v-x)
Comme on a :
x un réel de l'intervalle ]u;v[.
alors u < x < v qui donne : (x-u) > 0 donc positif et (v-x) > 0 aussi
donc le produit (x-u)(v-x) est > 0
donc :
yQ-x² > 0
merci beaucoup!!
j'ai presque tout compris!!
mis à part:
a=(yN-yM)/xN-xM)=(v²-u²)/(v-u)=[(v+u)(v-u)]/(v-u)=v+u (ou : u+v)
moi j'ai appris: (xN-xM)/(yN-yM)
et non l'inverse...
alors pourquoi le faire dans ce sens là?
moi j'ai appris: (xN-xM)/(yN-yM)
et non l'inverse...
alors pourquoi le faire dans ce sens là?
Le "a" de y=ax+b est tjrs avec les ordonnées au numérateur et les abscisses au dénominateur. TOUJOURS.
Tu dois confondre avec les coordonnées d'un vecteur.
Avec A(xA;yA) et B(xB;yB) on a les coordonnées du vect AB ainsi :
AB(xB-xA;yB-yA).
A+
excusez moi d'intervenir :§
J'ai aussi ce problème à faire mais je ne comprends pas le b)...
Je vous remercie
Lunie
Bonjour Lunie (pour toi donc qq. explications supplémentaires) :
on a vu au a) que :
Cette droite (MN) avec M et N , 2 points de la parabole P a donc une équa de la forme :
y=(u+v)x+b
Elle passe par le point M(u;u²) donc on peut écrire , en remplaçant x par u et y par u² :
u²=(u+v)*u+b qui donne b=u²-(u+v)u
Donc l'équa de (MN) est : y=(u+v)x +u²-(u+v)u
b) Il faut déjà comprendre que la parabole n'est pas tracée sur le graph que tu vois plus-haut.
P est un point de la parabole dont l'équa est : y=x².
Donc comme l'abscisse de P est x, son ordonnée est x². OK ?
Donc yP=x²-->ligne 1
Q est un point de la droite (MN) mais qui est sur la même "verticale" que le point P donc il a même abscisse "x" que P.
La droite (MN) a pour équa : y=(u+v)x +u²-(u+v)u
Pour trouver l'ordonnée de Q , on va utiliser cette équation en laissant le x qui est l'abscisse de Q ( et aussi de P) :
yQ=(u+v)x+u²-(u+v)u--->on développe :
yQ=ux+vx+u²-u²-uv
yQ=ux+vx-uv--->ligne 2
Avec lignes 1 et 2 , on calcule yQ-yP :
yQ-yP=ux+vx-uv-x²-->ligne 3
On demande de vérifier que yQ-x²=(x-u)(v-x) :
On développe donc (x-u)(v-x) qui donne :
(x-u)(v-x)= xv-x²-uv+ux soit : ux+vx-uv-x² qui est bien la ligne 3.
Donc yQ-x²=(x-u)(v-x)
D'après l'énoncé :
On note x un réel de l'intervalle ]u;v[.
ce qui veut dire : u < x < v
Comm u < x , alors (x-u) > 0
Comme x < v , alors (v-x) > 0
donc le produit (x-u)(v-x) est > 0 car les 2 facteurs sont positifs.
Donc :
yQ-x² > 0 mais x² , c'est yP
Donc :
yQ-yP > 0
Donc yQ > yP
Donc le point Q de (MN) est au-dessus du point P de la parabole.
Je ne peux pas faire plus !!
Désolé !!



