Inscription / Connexion Nouveau Sujet
Lemme de factorisation
Bonjour,
Voici l'énoncé :
Soit w
L(E,G) et vL(F,G)
Montrer que Ker(v)
Ker(w) ssi 
uL(E,F) telle que w=u°v
J'ai d'abord essayé de raisonner dans le cas où u et v sont des endomorphismes de E. Des recherches sur Internet m'ont suggéré de m'intéresser à l'endomorphisme induit sur un supplémentaire de Ker(v), mais je ne vois pas comment faire... Je comprends que l'on peut définir une fonction réciproque sur l'image de ce supplémentaire, mais pourquoi poser u= l'application nulle quand on ne se trouve plus sur cet espace ?
Pour le cas précis de l'énoncé, une indication suggère de passer par la représentation matricielle de w et v dans des bases B,D et C adaptées. On aurait alors MatB,D(w)=(O|A), et MatB,C(v) triangulaire supérieure par bloc, avec M inversible dans le bloc. Mais je ne vois pas où cela me mène...
Merci d'avance !
salut
J'ai d'abord essayé de raisonner dans le cas où u et v sont des endomorphismes de E.
Soit w
L(E,G) et vL(F,G)
Montrer que Ker(v)
Ker(w) ssi uL(E,F) telle que w=u°v
Ker v est un sous-espace de F
Ker w est un sous-espace de E
je ne vois pas trop comment on peut les comparer si E et F sont distincts ...
Merci pour ta réponse.
salut
je ne comprends pas trop puisque ce n'et pas le cas de l'énoncé ...
C'était essentiellement pour pouvoir se ramener à un cas plus simple (sans changement de base notamment) histoire de pouvoir écrire quelque chose et progresser un peu dans les idées...
je ne vois pas trop comment on peut les comparer si E et F sont distincts ...
Je suppose qu'avoir l'inclusion d'un Ker dans l'autre suffit à écrire une base adaptée, et qu'on s'en sort avec les matrices de passage ?
Merci d'avance pour votre aide !
Bon, d'un point de vue matriciel, à tête reposée, j'ai peut-être quelque chose...
Je n'arrive pas à écrire des matrices par blocs sur le forum avec Latex (message d'erreur), donc je n'ai qu'une image désolé...
Tout d'abord considérons un supplémentaire de Ker(v) tq Ker(v)
A=F
On peut également écrire, par inclusion, que Ker(v)C= Ker(w)
Considérons un supplémentaire de Ker(w) tq Ker(v)CD=E
Alors dans des bases adaptées : (M inversible par théorème d'isomorphisme )
Annuler
connectez vous
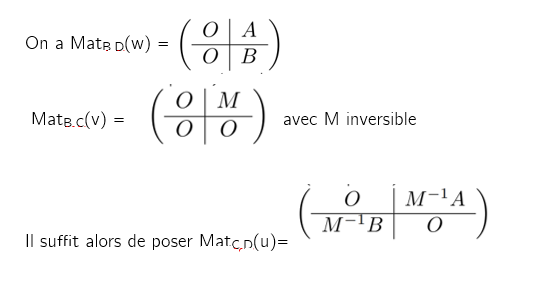
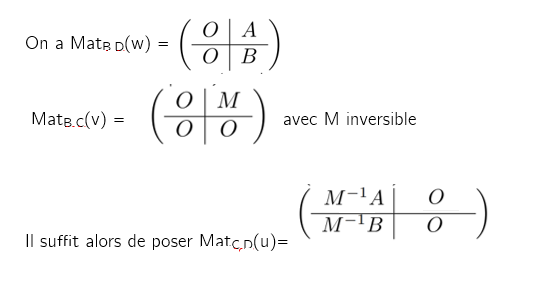
algèbre en post-bac