J'espère que ça marche...

bonjour

il semblerait qu'il y ait une erreur dans ton énoncé : O'1 O= a+b-R
par ailleurs, ton énoncé est-il bien complet ?
as-tu essayé de construire les cercles jumeaux ?
parce qu'il me semble que le triangle O1 O O'1 n'est PAS rectangle en O,

en construisant le dessin, on voir apparaitre un point H[AB], différent du point O, tel que O1HO'1 est rectangle en H   (donc h = HO'1)
fais une petite recherche pour trouver la construction du dessin pas à pas.

pour montrer que h² =4Ra ou h²= 4b(a-R) , c'est du calcul littéral avec les données présentes dans l'énoncé.

j'espère t'avoir aidé

Bonjour,
il faudrait déja définir a et b

vu la 1ère formule on peut deviner que a et b sont les rayons des deux cercles de centres O₁ et O₂

illustration du point H peut être :



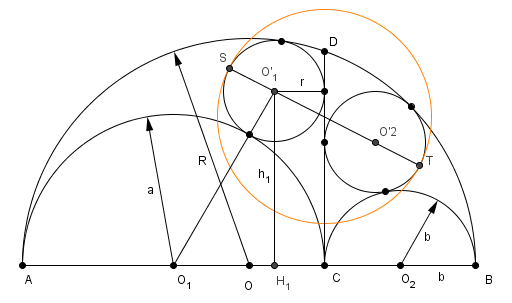
h² = 4Ra me semble bien faux !!
h² = 4b(a-R) encore plus vu que ça donnerait un carré h² < 0 puisque a < R !!
(je l'ai appelé h₁ vu que c'est lié spécifiquement au cercle (O₁)

R = 3, a = 2 donne 4Ra = 24
mais une mesure de h₁ donne h₁ = 2.31 !!

donc de quel triangle parle l'énoncé exactement et de quelle hauteur, mystère et boule de gomme...

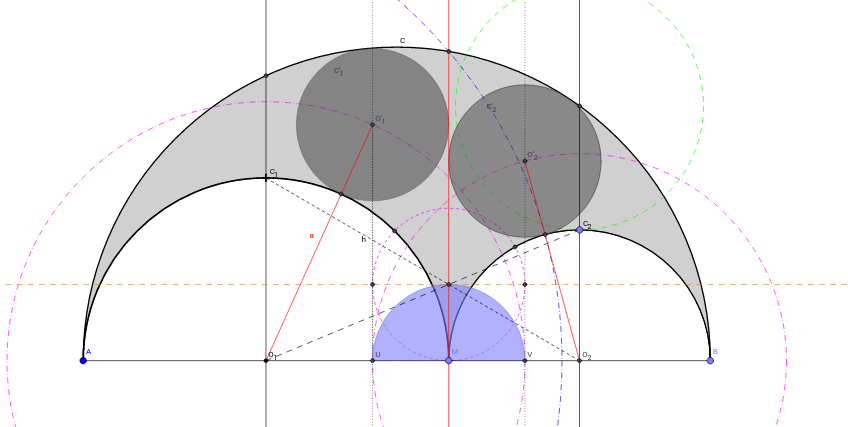
nota : parmi les innombrables propriétés et constructions de ces cercles jumeaux, le cercle ici en orange a un diamètre = ST = CD ! (le démontrer)

je pense avoir saisi cette histoire de triangle O₁OO'₁

c'est bien ce triangle là, qui n'est pas rectangle pour un sou, et dont la hauteur O'₁H est "intéressante" :



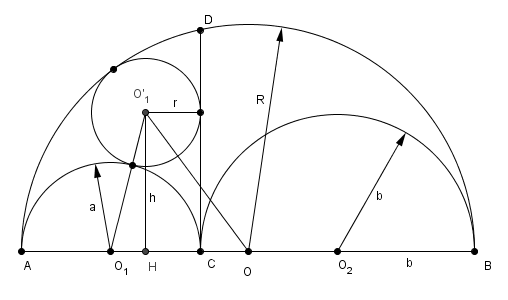
en effet en écrivant cette hauteur par Pythagore dans les deux triangles rectangles (en H !) O₁HO'₁ et OHO'₁, l'égalité de ces deux expressions donne ce qu'on cherche, à savoir r(a+b) = ab après toutes les simpliications

commencer par exprimer toutes les longueurs concernées en fonction de a, b et r seulement
R = a+b (ne pas confondre r et R !!)
O₁O'₁ = a + r
OO'₁ = R - r = a + b - r
O₁H = O₁C - CH = a - r
etc

bonjour Mathafou !  j'aurai dû parier vous croiser sur ce topic
perso, je ne suis pas partie sur les mm bases que vous, mais j'avoue ne pas avoir su tout  éclaircir...

j'avais interprété que a=AC et b=CB
R étant le rayon des cercles jumeaux
apparemment, avec cette base, on a bien les formules données pour h

pour la construction, j'ai fini par trouver un .pdf sur internet qui explique les étapes
(ai-je le droit d'en mettre le lien?)

en bref, pour trouver le rayon, on détermine un point K par construction, lequel nous donne avec Thalès l'égalité R = CK = ab/(a+b)
puis on en déduit les positions de H1 et H2 (cercle vert)

pour les centres des cercles jumeaux, on trace les cercles rouges, et par intersection, on trouve O1 et O2.

je vous laisse la main si vous souhaitez poursuivre.
bonne fin de journée.

désolée, je n'avais pas vu votre message.
nous ne sommes pas partis avec le mm R.
avec "le mien", je trouve OO'1 = a+b-R et OH1 = a-b-R  (?)

erreur de saisie de ma part, lire : a=AC/2 et b=CB/2

Pas de problème, répondra celui qui a envie de répondre ou d'ajouter quelque chose.


OK pour le coup de R et r, c'est moi qui ai mal lu le message d'origine R = ab/(a+b) définit bien R comme rayon des cercles jumeaux
(dont on ne sait pas encore qu'ils sont égaux !!)
mon R = rayon du cercle de diamètre AB étant un peu inutile vu que c'est directement = a+b !!
d'ailleurs ça s'élimine immédiatement dans ce que j'ai écrit.


j'ai la même construction que dans ton pdf apparemment. (doit bien être un grand classique)
mais il ne s'agit absolument pas de partir de cette construction pour démontrer la formule, vu que bien au contraire c'est à partir de la formule qu'on a obtenu cette construction !

donc partir absolument pas d'une construction, mais d'un calcul à partir de Pythagores sur la hauteur de OO₁O'₁
(parler de Pythagore ne fait pas de ce triangle un triangle rectangle ! mais la juxtaposition de deux triangles rectangles dans lesquels on applique séparément Pythagore)

et c'est ce calcul qui :
- aboutit bien à h² = 4ra d'une part et h² = 4b(a-r) d'autre part (avec ma notation r que je laisse écrite ainsi car j'ai parlé de R avant)
- donnera donc la formule r = ab/(a+b) pour le cercle de centre O'₁
- et par conséquent l'égalité des deux cercles jumeaux (vu que c'est symétrique en a et b on aurait obtenu la même formule pour l'autre cercle)

la balle est maintenant dans le camp de momopeixinho pour effectuer les calculs détaillés, maintenant que c'est clarifié avec précision explicite du pied de la hauteur H

Bonne nuit,

Pour établir la formule de R (rayon des cercles jumeaux) et démontrer qu'ils ont le même rayon,
j'utilise une inversion de centre A et puissance AC² et une inversion de centre B et puissance BC².
J'applique alors : Le centre du cercle inverse d'une droite est le conjugué du symétrique du pôle par rapport à la droite.
Ce qui situe facilement H₁ et H₂ par rapport à C.

Mais pour momopeixinho l'inversion n'est plus au programme du lycée en France !

avec les deux Pythagore c'est fait en quelques lignes.
à momopeixinho de les écrire
et d'abord de formuler correctement en fonction de a,b et R (R notation d'origine) tous les côtés concernés
on les a tous donné ici au cours de la discussion, si momopeixinho a quelques doutes il peut les exprimer.

nota 1 : OH₁ = |b-a+R| car c'est une longueur, c'est tout aussi bien |a-b-R|
de toute façon c'est sans importance vu qu'on n'utilise que son carré.

ce calcul s'avère donc en fait de niveau fin de collège ! (sommes et différences de longueurs, Pythagore, différence de deux carrés A² - B² = (A+B)(A-B), ou développement de (A±B)², manipulation d'expressions)

Nota 2 : l'inversion est une autre façon de construire les cercles jumeaux sans utiliser la relation qu'on veut démontrer ici
en utilisant une inversion de centre C qui échange A et B (ce qui va faire hurler les anglophones, une puissance négative) on transforme le problème en :
construire un cercle tangent à deux droites parallèles et à un cercle donné.



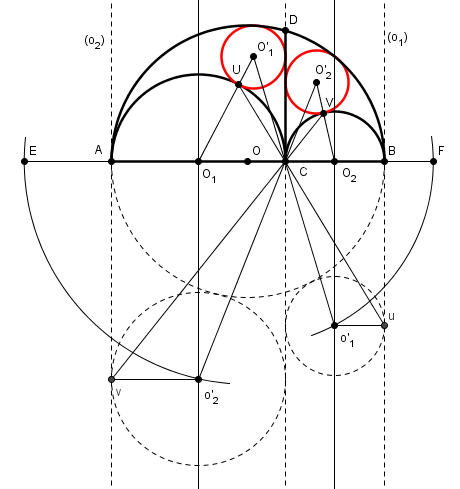
les éléments en pointillés et en lettres minuscules sont les images par inversion des éléments de l'arbelos

l'image du cercle (O₁) est la droite (o₁) : (O₁) passe par C et l'inversion échange A et B.
l'image du cercle cherché (O'1) est donc un cercle tangent à (O) (conservé par l'inversion), à cette droite (o1) et à la droite (CD), conservée par l'inversion.
ce qui est un problème archi-classique : le rayon de (o'₁) est égal à b, le centre o'₁ est donc l'intersection de la médiatrice de BC et du cercle de centre O et de rayon OB + b = OF
et pareil pour l'autre

les points de contacts u et le centre o'₁ sont ensuite ré-inversés pour donner U et O'₁ à la règle seule.

on peut aussi utiliser l'inversion de centre A et de puissance AC² (qui conserve C) mais l'image des cercles (O) et (O₂) est moins commode à tracer vu qu'il faut construire l'image de B d'abord.

Bonsoir à tous,
Merci pour vos informations mais je crois que nous n'étions pas sur la même longueur d'ondes pour l'histoire du triangle rectangle. J'ai du mal m'exprimer veillez m'excuser (ma langue naturelle n'set pas le français ).
Je reprends :
Nous travaillons sur le triangle rectangle O'1 HO,
je cherche à démontrer que h^2=4b(a-R)
On est d'accord que R est le rayon des cercles jumeaux d'Archimède.
De plus, R=ab/(a+b) et h=2a racine de b/(a+b)
Je souhaite juste, après une recherche sur le net par curiosité savoir comment on peut démontrer cela.
Je vais essayer de joindre un schéma....

Etant donné que mon image est trop grosse et que je ne sais pas réduire, je vous met le lin de mon schéma qui se trouve sur Géogebra :

https://ggbm.at/DUnxyM6d

J'espère que cela fonctionne....

***citation inutile supprimée***
*Dans le schéma dans le lien,  U est O et le point O appartient à UM

pourquoi tu dis que ça passe pas ?

Merci
Cela doit être mon ordinateur
J'ai essayé de démontrer R=...
Le diamètre des cercles jumeaux d'Archimède vaut  d= (AM×MB)/AB
On a donc :
R=((2a×2b)/2a+2b)/2
R=(ab) /(a+b)

Et pour h : la distance entre ces cercles et la droite AB vaut racine de AM ×d
Soit :
h= racine de 2a ×((2a×2b)/2a+2b)/2
h= 2a racine de b/(a+b)
Je pense que c'est un peut simple mais je ne vois pas comment faire sutrement.

attention, que comme déja dit la construction proposée ne peut absolument pas servir à faire une démonstration vu que c'est le contraire :
c'est à partir de la relation R = ab/(a+b) (démontrée au préalable !!) que l'on a "fabriqué" artificiellement cette construction (par la construction de R à partir de la relation).

reprenons au départ sur des bases logiques saines :
on ne connait aucune des relations citées
on ne sait pas que les deux cercles sont égaux
et on ne sait pas non plus les construire

c'est ça le vrai point de départ
tout le reste est à démontrer.


pour démontrer la relation R = ab/(a+b) (on ne la connait pas à priori !!) le plus simple (niveau collège disais-je) est de calculer h² par les deux triangles rectangles précités, qui existent sur la figure indépendamment de toute méthode de construction. (= la figure de l'énoncé)
avec ma figure du 10-10-16 à 17:04 en virant R et en appelant R = rayon des cercles jumeaux, pour l'instant du seul cercle de centre O'₁ (vu qu'on ne sait pas encore qu'ils sont égaux)

O₁O'₁ = a + R (cercles tangent extérieurement)
OO'₁ = (a + b) - R (cercles tangents intérieurement, le grand cercle de centre O a pour rayon a+b
O₁H = O₁C - CH = a - R (simple soustraction de longueurs)
OH = OA - AC + CH = (a+b) - 2a + R = |b-a+R| (idem)

Pythagore dans O₁O'₁H donne h² = (a + R)² - (a - R)² = 4aR (en développant)

et d'une

Pythagore dans OO'₁H donne h² = ((a + b) - R)² - (b - a + R)²

on peut développer (long) ou plus astucieusement écrire cela sous la forme
h² = (b + (a-R))² - (b - (a-R))² = 4b(a-R)
(on applique l'identité remarquable (X+Y)² - (X-Y)² = 4XY déja "observée" pour le calcul précédent)

et de deux

reste la troisième, la formule qui donne R qui est une conséquence (et pas une cause) de ces deux relations
h² = 4aR = 4b(a-R)
donne (déja on simplifie par 4), on regroupe les R du même côté :
(a+b)R = ab et donc R = ab/(a+b)

terminé.

et donc maintenant qu'on sait cela on en déduit :
- que les deux cercles jumeaux sont égaux car si on avait calculé le rayon de l'autre on aurait obtenu R' = ba/(b+a) qui est la même chose
- une construction possible en construisant la mesure de R = ab/(a+b)
(alias 1/R = 1/a + 1/b) (avec le coup des deux échelles qui se croisent, démontrées par Thalès)
ou une autre méthode qui revient plus ou moins au même pour construire 1/R = 1/a + 1/b

Bonjour,

A mathafou : Ce qui est très gênant dans votre façon de procéder, c'est que vous n'avez pas montré, dans votre figure du 10-10-16 à 17:04 que vous pouviez appliquer :
OO'1 =  (a + b) - R  (cercles tangents intérieurement, le grand cercle de centre O a pour rayon a+b
Et je ne vois pas comment le montrer "au niveau collège", car si on "voit bien" que le cercle de centre O'1 peut rouler sur le cercle de centre O1 pour venir s'appuyer sur le segment [CD], il n'est pas montré que ce cercle est alors justement tangent aussi au cercle de centre O.

Je pense que vous ne pouvez éviter de considérer une inversion de centre A et puissance AC² qui résoud la construction du cecle de centre O'1 et établit immédiatement la formule du rayon en considérant le conjugué de B par lequel une parallèle à [CD] est tangente au cercle de centre O'1.

Il me semble que les propriétés de l'inversion qui sont alors utilisées sur cette figure peuvent être établies avec les quelques éléments de géométrie connue au lycée...

Désolé mais il me semble que la propriété "cercles tangents <==> distance entre les centres = |R ± r|" est du B-A-BA de collège sur la définition même de "cercles tangents" (voire même en tout début de collège)


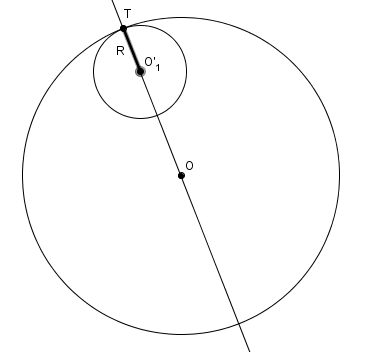
que OO'₁ = OT - O'₁T relève de la définition de cercles tangents
OT est le rayon, du grand cercle de centre O

et que ce rayon du grand cercle soit = a+b est une autre "évidence" par simple somme de longueurs

le diamètre du grand cercle est AB = AC + CB = 2a + 2b = 2(a+b) et donc son rayon est la moitié de son diamètre = a+b



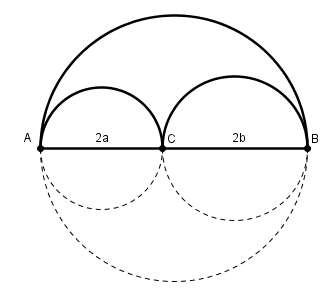
et donc OO'1 = (a+b) - R "de façon évidente"


ni CD ni le cercle de rayon a, aussi tangents au cercle jumeau cherché, n'ont leur mot à dire dans l'expression OO'₁ = (a+b) - R

tout est à ce niveau dans cet exo et rien qu'à ce niveau.

une fois qu'on a calculé toutes les longueurs ainsi (simple sommes et différences d'autres longueurs et rien d'autre)
affirmant séparément que le cercle cherché est tangents à chacun trois trucs individuellement,
alors on écrit que l'ensemble de ces relations doit être satisfait ce qui donne une sorte de système d'équations (on peut le considérer ainsi) dont les inconnues sont R et OO₁, OO'₁ etc
et le calcul (avec Pythagore) a pour but d'éliminer les inconnues auxiliaires pour ne garder que l'inconnue R

Rebonjour,

J'ai effectivement tort : On sait construire un cercle tangent aux cercles de centres O et O1 et qui vienne s'appuyer sur [CD] en étant tangent à [CD].
Votre système d'équations répond alors bien à la question.
Je le trouvais juste un peu long à mon goût.

il n'y a pas plus simple si on détaille tout, et à ce niveau (Lycée).

il faut juste bien voir, comme d'hab, quelle sont les hypothèses, de quoi on part et où on veut arriver.
en évitant soigneusement de prendre ses désirs pour des réalités (croire que quelque chose est vrai simplement parce qu'on l'a écrit, ou simplement parce que c'est ce que demande de prouver l'énoncé) et de faire des raisonnement circulaires (partir d'une formule pour aboutir à la même formule sans avoir rien démontré en fait)

ici on part de la seule figure d'origine (du post initial) prétendant l'existence de ces cercles, et on ne sait rien de plus
aucune des formules indiquées à ce moment (ce sont des formules toutes à démontrer) ni aucune construction, ni même si c'est possible
(le fait que l'on puisse en calculer le rayon sera la preuve de leur existence)

et la formule donnera une construction effective, par une construction construisant cette valeur de rayon là, obtenue par la formule démontrée au préalable.