Inscription / Connexion Nouveau Sujet
les dérivées Terminale S
Coucou les ami(e)s !
Voilà j'ai deux exercices sur les dérivées, j'ai essayé de les faire, je vais vous faire part, de mes résultats,
mais je doute un peu que ce soit bon.. Donc j'aimerai que vs me vérifiez et que vous m'expliquiez si jamais j'ai une erreur, svp ^^
Alors voilà l'énoncé 1 :
Soit la fonction f définie sur R/(2)
f(x) = (3x-4)/(x-2)
a) déterminer la fonction f' dérivée de f.
b) En déduire la fonction dérivée des fonctions :
g(x) = (3 sqrt(x) - 4)/(sqrt(x) - 2)
h(x) = (3cosx - 4)/(cosx - 2)
Enoncé 2 :
Soit f la fonction définie sur R :
f(x) = -x + sqrt(x^2 + 8)
et C sa courbe représentative dans le plan muni d'un repère
a) Démontrer que f est décroissante sur R à l'aide su signe de f'(x)
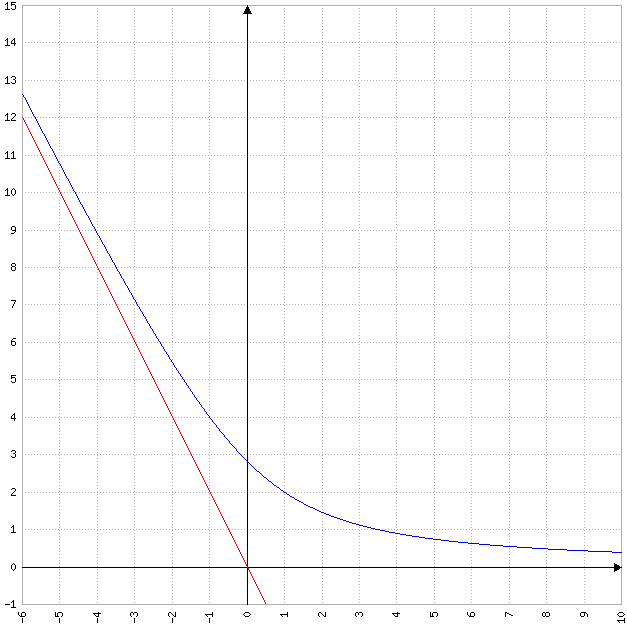
b) Etudier les limites de f en +infini et -infini et démontrer que la courbe C représentative de f admet pour asymptotes la droite y= -2x et l'axe des abscisses.
c) Tracer C dans un repère orthonormal (On prendre 2cm pour unité graphique)
__________________________________________
Mes réponses à l'énoncé 1 :
a) Après calcul de la dérivée, je trouve f'(x) = -2/(x-2)^2
la dérivée est-elle bonne ???
b) Je ne vois pas comment déduire de f'(x) les dérivées g'(x) et h'(x)
Sachant ne pas trop comment partir de f'(x), j'ai donc adapté la même démarche de calcul de dérivée que pour le a)
Au final , j'ai g'(x) = -1/[sqrt(x)(sqrt(x) - 2)^2]
h'(x) = 2sinx/(cosx-2)^2
Donc voilà je ne vois pas trop le lien :S
Il manque un - je suppose dans h'(x), et pour g'(x) je crois que c'est pas bon.
Mes réponses à l'énoncé 2 :
pour l'instant j'ai fait que la a) car j'aimerai savoir comment justifier que le signe de f'(x) est tjrs positif pour tout x appartenant à R
Concernant la dérivée j'ai trouvé : f'(x) = - (sqrt(x^2 + 8) + x)/(sqrt(x^2 + 8)
Est-ce bon ?
________________
Voilà voilà ^^
Merci pour votre aide !
Passez une bonne soirée !
Bonjour,
Hou là là ....
Une question après l'autre  , c'est toujours difficile de prendre le truc avec autant d'éléments ...
, c'est toujours difficile de prendre le truc avec autant d'éléments ...
Bon, je regarde.
oui je vois, a la place de x ya racine de x et cos x,
les dérivées que j'ai calculé pour g'(x) et h'(x) sont bonnes ?
Non, tu ne peux pas simplement remplacer x par  x par exemple, ça ne marche pas comme ça.
x par exemple, ça ne marche pas comme ça.
[fog(x)]' = f'og(x)· g'(x)
dans ce cas :
(fog)'(x) c'est avec f(x) = (3x-4)/(x-2)
et dans ce cas g(x) c'est quoi ? racine de x?
daccord ! je comprends !!!
mercii !!
Et je suppose que c'est pareil avec h(x) ou h'(x) = cos x ^^
merci bcp !!
Peux tu m'aider pour le 2e exo ??
donc on a
(f o g)(x) avec f(x) = (3x-4)/(x-2) et g(x) = racine de x
(f o g)'(x) = g'(x) X f'(g(x)) [avec g'(x) = 1/2racinex et f'(x) = -2/(x-2)^2
ce qui donne :
(f o g)'(x) = 1/2racinex X (-2/(racinex-2)^2)
(f o g)'(x) = -2/[(2racinex)(racinex-2)^2)]
(fog)'(x) existe si et seulement si (2racinex) et (racinex-2)^2) différent de 0
je suis sur la bonne voie ???
Je n'ai pas vérifier, mais l'idée a l'air bonne.
Par contre, le domaine de définition par rapport à mon post de 20:23, il est où ?
le domaine de def final,
je pense que ce serait :
D(fog)
<=> x € Dg tel que g(x) € Df
<=> x € R+ et g(x) € R/(2)
<=> x € [- infini ; 2[U]2; + infini]
Donc D(fog) = [- infini ; 2[U]2; + infini]
c'est bien cela ?
Tu recherches le domaine.
Il faut donc x 0 et
0 et  x
x 2
2
A opartir de là, 2 solutions pour calculer la dérivée.
Soit tu dérives à partir de cette expression première de g(x), soit tu utilises [uov(x)]' = u'ov(x)· v'(x)
Et comme dans ta question on te dit "En déduire", c'est donc par la 2ème solution qu'il est préférable de passer ...
Tu remarqueras au passage, que ta fonction
était défnie en x=0.
par contre ta dérivée :
n'est pas dézrivable en x=0.
Pour être plus rigoureux : la fonction g (et non pas g(x) ) est définie en 0, mais elle n'est pas ddérivable en 0.
La fonction g', dérivée de la fonction g (et non pas la fonction g'(x) ) n'est pas définie en 0.
Oui.
Soit tu dérives à partir de cette expression première de g(x), soit tu utilises [uov(x)]' = u'ov(x)· v'(x)
Et comme dans ta question on te dit "En déduire", c'est donc par la 2ème solution qu'il est préférable de passer ...
Attention à ton domaine de définition au préalable.
coucou alors voilà ce que j'ai fait pour h(x)
h(x) = (3cosx -4)/(cosx-2)
Df=R
On pose h2(x) (jai mis h2(x) pour pas que l'on confonde avec h(x)) = cos x
Df = R
On a donc h(x) = (f o h2)(x) = f(h2(x)) = f(cos x)
h est dérivable sur R comme composée de fonctions dérivables.
Vx€R, h'(x) = (f o h2)'(x) = h2'(x) . f'(h2(x))
(f o h2)'(x) = - sinx . -2/(cos x-2)^2
(f o h2)'(x) = 2sinx/(cosx - 2)^2
Donc h'(x) = 2sinx/(cosx - 2)^2
Niveau rédaction et dérivée c'est bon ??
J'ai procédé de la même manière pour g(x), même rédaction (qq changement au niveau du domaine de définition qui est différent) sinon la procédure est la même.
hourraaa !!!
et pour l'exo 2 ??
je voudrais juste savoir si possible, si la dérivée est bonne,
et si oui comment justifier qu'elle est strictement décroissante sur R.
Après je pense que les limites et la représentation graphique ça devrait aller ^^
Je te les enverrai quand même, on sait jamais.
voilà ma démarche pour le calcul de dérivée.
f(x) = -x + sqrt(x^2 + 8)
Df = R
f est dérivable sur R comme somme et composée de fonctions dérivables sur R.
f = u + v donc f' = u' + v'
avec u'(x) = -1
v'(x) = x/sqrt(x^2 + 8)
on a donc f'(x) = -1 + x/sqrt(x^2 + 8)
j'ai mis au même dénominateur, ce qui donne
f'(x) = - [sqrt(x^2 + 8) + x]/sqrt(x^2 + 8)
pour simplifier, je ne sais pas si j'ai bien fait, mais j'ai enlevé les racines avec l'expression conjuguée.
ce qui donne : - [sqrt(x^2 + 8) + x]/sqrt(x^2 + 8) . [sqrt(x^2 + 8) - x]/[sqrt(x^2 + 8) - x]
<=> - [(x^2 + 8) - x^2]/[x^2 + 8 - x] (en simplifiant les racines)
<=> - 8/[x^2 - x + 8]
le signe de f'(x) dépend donc du dénominateur.
calcul de delta.
delta < 0
donc aucunes racines.
donc [x^2 - x + 8] > 0 pour tout x€R
Ainsi - 8/[x^2 - x + 8] < 0
<=> f'(x) < 0 pour tout x€R
f'(x) est donc décroissante sur R.
C'est bon niveau rédaction et solution ?
pour les limites en l'infini, j'ai trouvé :
lim f(x) = +infini (j'ai levé l'indétermination inf-inf par expression conjuguée)
x->+inf
lim f(x) = + infini
x->- inf
J'ai vu une représentation graphique de la fonction, j'observe bien les asymptotes énoncées mais je ne vois pas comment les repérer par le calcul..
y = 2x je sais que c'est une asymptote oblique.
je crois que c'est f(x) - (ax +b) = 0
et l'axe des abscisse, c'est pas sensé être une asymptote horizontale ?
seulement j'ai vu que l'asymptote horizontale c'est uniquement quand lim f(x) en + ou - infini est égale à un réel b . Dans ce cas, le réel ce serait +infini (par rapport aux lim calculées précédemment) ??
Je pense que tu as commis une erreur en multipliant par l'expression conjuguée.
En effet, si tu trouves bien -8 au numérateur, par contre le dénominateur ne se simplifie pas ainsi.
et cela se simplifie beaucoup moins.
A mon sens, ce qu'il faut faire, c'est rester sur l'expression :
et raisonner ainsi :
Le dénominateur est >0 sur  , donc le signe de f'(x) ne dépend que du numérateur.
, donc le signe de f'(x) ne dépend que du numérateur.
Or,
Or, sur

donc :
 si x>0, on a :
si x>0, on a :
et comme on a vu que sur

On a pour x>0
 si x<0, on a :
si x<0, on a :
or, l'expression entre parenthèses avec radical est > 0 (elle est même >2 vu que sur
 ), le signe de f'(x) ne dépend plus que de x.
), le signe de f'(x) ne dépend plus que de x.
Comme ici on est avec x<0, là aussi on a pour x<0
donc f est décroissante sur  .
.
Ok ? 
Pour les asymptotes, tu as plusieurs façon de faire.
Regarde le lien ci-dessous et mon post à 23:11 qui explique l'une des méthodes pour déterminer les équations des asymptotes à une courbe..
Vois si "ça te parle", et fait moi signe.
![]() Déterminer une équation asymptote
Déterminer une équation asymptote
Avec la méthode exposée dans mon lien, pour m tu dois trouver m=-2, et pour p tu dois trouver p=0.
Donc l'équation de l'asymptote sera
Pour mon post de 06:30 ci-dessus, il s'agit de la recherche quand x -
- bien sûr.
bien sûr.
Tiens-moi au courant.
Léo 
tu te lèves de bonne heure toi ! ^^
bon pour le signe de f'(x), tout est ok, j'ai tout compris 
En suivant ta méthode des asymptotes,
Soit (d) la droite d'équation y=mx+p
On a lim f(x) = +infini
x-> -infini
Déterminons m, lim f(x)/x = [-x + sqrt(x^2 + 8)]/x
après factorisation, réduction,... ect...
je trouve que lim f(x)/x = -2(sqrt(1 + 8/x^2))
or, lim 1 + 8/x^2 = 1
x -> -inf
et lim sqrt(y) = 1
y->1
Par composition, lim sqrt(1 + 8/x^2) = 1
quand x -> - inf.
De plus, lim -2 = -2
x->-inf
Par produit, lim -2(sqrt(1 + 8/x^2)) = -2
On a alors, (d):y=-2x+p
Calculons p :
lim (f(x)-mx)=p
lim (f(x)+2x)= -x + sqrt(x^2 + 8) + 2x
lim (f(x)+2x)= x + sqrt(x^2 + 8) [je lève l'indétermination par expression conjuguée]
lim (f(x)+2x)= (x^2 - x^2 - 8)/(x - sqrt(x^2 + 8))
lim (f(x)+2x) = -8/(x - sqrt(x^2 + 8))
Or, lim -8 = -8
x-> -inf
[.... là je détaille ....]
et je trouve bien
lim (f(x)+2x) = 0
x-> -inf
Au final, on a alors : (d):y=-2x
La courbe C admet donc une asymptote oblique d'équation y=-2x
Donc pour ça, c'est bon ??
Et puis pour l'axe des abscisses, comment dois-je procéder ?
... et j'étais déjà levé depuis 1 heure ...
Pour lever les indéterminations, tu pouvais aussi faire comme dans mon poste de 60:19, plus facile.
Pour la 2ème asymptote, tu procèdes pareil.
oui c'est ce que je vais faire c'est plus court et plus simple.
donc en fait je procède de même, avec une équation de droite ?
ce qu'on a fait c'est pas SEULEMENT pour asymptote oblique ??
Ce que j'ai appris c'est que pour une asymptote horizontal,
on doit démontrer que lim f(x) quand x -> + ou - infini = a
dans ce cas, la valeur a serait +infini ??
vu que lim f(x) quand x -> + infini et - infini = + infini . ??
ou alors la droite d'équation y=0 !
dans ce cas,on fait les mêmes calculs, avec m = 0 et p=0
c'est ça ??
En fait, tu vas directement trouver
Donc y=0 est asymptote à la courbe.
Tu ne fait avec m et p que quand tu trouves

 x
x