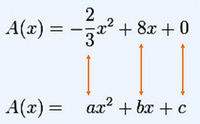Inscription / Connexion Nouveau Sujet
Les Fonctions (seconde)
Bonjour,Voila je vous expliques j'ai un Dm de Maths pour mardi 17 avril et je vous avoue que je n'ai pas du tout compris la leçon qui porte sur les fonctions carré,les fonctions polynomes de dergré 2 et les fonction homographique ce qui fait que mon Dm je ne l'ai pas compris non plus et je suis très embêter c'est pour cela que je demande de l'aide svp ...
Enoncé:
On considère une fenêtre sous un toit incliné.le but de l'exercice esr de déterminer les dimensions de la fenetre assurant le plus de luminosité.On cherche donc le x et le y pour lesquels l'aire de la fenetre (A(x)) sera maximale.
On donne:OA=8m et OB=12m
(shéma ci dessous)
1) Exprimer NA et NM en fonction de x et de y et des données de l'énoncé. en déduire l'aire du triangle ANM notée Aanm.
2)Exprimer PB et PM en fonction de x de y et des données de lénoncé. En déduire l'aire de PMB noté Apmb.
3)l'aire du rectangle MNOP sera noté A(x). Exprimer A(x) en fonction de x et y.
4)a) Que vaut l'aire du triangle AOB,noté Aaob ? (utilisé les données de lénoncé)
b)On remarque que Aaob = Aanm +A(x) + Apmb
En remplaçant chacun des termes de cette équation par leur expression trouvée dans les questions 1,2 et ,montré que l'équation ci dessus se simplifie en équation suivante : 48=4x + 6y .
c)Déduire de léquation ci dessus une expression de y rn fonction de x .
5) Remplacer y par son expression trouvée a la question 4)c),dans A(x). En développant monterer que A(x) =8x-2/3x au carré.
6)a) A(x) étant de la forme ax au carré + bx + c identifier les coefficients a,b et c .
Chercher les coordonnées du sommet S. Dans quel sens la parabole est t elle tournée ?
b)Chercher l'intersection de la parabole avec l'axe des ordonnées et celui des abcisses.
7)Calculer A(3) et A(9)
8)Pour quel x la fonction A(x) est elle maximale ? Quelle est la valeur maximal de A(x) ? Que represente Amax par rapport à Aaob ?
9)Conclure en donnant les valeurs de x et y pour lesquelles A(x)=Amax .
10) En utilisant les valeurs x et y pour lesquelles la luminosité entrant par l
fenetre est maximale,refaire le schéma de l'énnoncé.On prenfra comme échelle 1cm diviser par 2 m .
Voila les questions que je n'ai pas du tout compris,merci d'avance pour votre aide 
Alicia33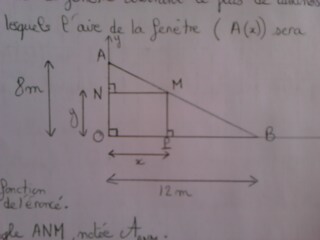
édit Océane : forum modifié
Bonsoir alicia33
L'aire d'un triangle est donnée par
1) NA= OA-ON=8-y
NM = x
Donc
2) Le raisonnement est analogue.
3) Evidemment,
etc...
Merci Hiphigenie J'ai compris pour l'aire 
Par contre la suite reste un mystère pour moi ... et je n'ai pas du tout compris le sens de la question b)
Donc, tu as compris et répondu aux questions 1), 2), 3) et 4a) ?
Qu'obtiens-tu pour la question 2 et pour la question 4a ?
C'est selon ces réponses que nous pourrons continuer. 
Oui,enfin je pense je suis pas sure pour la 1) le calcul reste le même non ? puisqu'on a pas de chiffres ?
la 2) c'est l'aire de PNM donc avec la même formule sa donne 12-x * y / 2 non ?
La 3) A(x) = x * y
4)a) Aire de AOB c'est 12*8/2 ce qui fait 48
Encore une fois je suis pas sure du tout de moi ...
Pourtant c'est correct si tu parles bien de l'aire du triangle PMB. 
b)On remarque que Aaob = Aanm +A(x) + Apmb
Je suppose que tu comprends cette phrase... sinon, regarde ta figure pour mieux comprendre.
Si on transcrit cette phrase avec nos résultats, nous aurons :
Tu développes tout ça et tu arriveras à
Ah ouiii c'est bon,parce que moi javais sauté une étape donc jarrivée pas a voir d'ou sorté le 48=4x + 6y mais maintenant c'est bon merci.
j'imagine que la suite et beaucoup plus compliquer ...
Et là je vois pas du tout ce qu'il faut faire ... je dois trouver la valeur pour 6y et pour y ? ou trouver le x et le y ?
Ok super merci
donc pour la 5) j'ai pas compris la question c'est à dire remplacer y par son expression trouvée en 4)c) donc on a trouvé 8-2x/3,dans A(x). En développant montrer que A(x)=8x-2/3x2 ?
On a : et
.
Tu peux ainsi répondre à la question 5...
... c'est-à-dire remplacer y par son expression trouvée
Donc si j'ai ien compris il faut remplacer le y dans l'expression A(x) = x*y
Ce qui donne A(x) = x*8-2x/3 ?
Ah non je l'ai pas encore calculé sa doit faire A(x) = 8x - 2/3x2 je pense et du coup on arrive sur la forme développer non ?
sa doit faire A(x) = 8x - 2/3x2 je pense
ben on a juste multiplier par x donc normal que sa soit la même expression mais au carré sa j'ai compris mais c'est le développement de l'expression ça ?
Ok oui c'est bon j'ai compris ça merci 
Donc pour la 6)a) A(x) de la forme ax2 + bx + c identifier les coeff a,b et c donc a=8 b=-2 et c=3 enfin je pense pas que sa soit ça le ax2 et bx m'embête un peu ...
Non, ce n'est pas ça, comme tu le dis si bien 
Nous avons :
Nous pouvons l'écrire autrement : .
Tu compares cette dernière expression avec en regardant les coeffcients de x², de x et le terme indépendant.
Que valent a ? b ? c ?
Ah oui c'est bon je vois pas pourquoi je me suis compliquer la vie moi aussi merci 
Donc a= -2/3 b= 8 et c= 0
Donc pour chercher les coordonnées du sommet S je sais pas du tout le faire je sais qu'il y a une histoire de alpha et beta ou de forme canonique ou avec la formule -b/2a ?
Alors...
La réponse pour n'est pas correcte non plus.
Si tu ne souhaites pas appliquer la formule que j'ai rappelée, tu peux le calculer autrement puisque
en fait j'ai pas calculé beta j'ai crus que parce que alhpa = 6 alors béta aussi mais c'est pas ça ...
Je comprends bien ton problème.
Alors, tu as eu largement le temps de calculer et de préparer la suite...
Que vaut ?
ok merci  mais je dois mal faire le calcul parce que je retombe sur 10.6 sa m'ennerve ...
mais je dois mal faire le calcul parce que je retombe sur 10.6 sa m'ennerve ...
oui mais j'ai pas compris après A(6)= il était censé y avoir quoi ?
La valeur de !
On a :
Comme l'abscisse du sommet est , on peut trouver l'ordonnée de ce sommet en remplaçant x par 6 dans cette expression, soit calculer
Oui !
Pour la fin de cette question, regarde ceci :
Si a > 0, alors le trinôme du second degré f(x) = ax²+bx+c admet un minimum
Si a < 0, alors le trinôme du second degré f(x) = ax²+bx+c admet un maximum
Quelle est notre situation dans l'exercice ?