Inscription / Connexion Nouveau Sujet
Les matrices...
CouCou 
Voici deux exercices traitant des matrices que j'ai à faire.
J'ai quelques difficultés car je comprends les consignes mais...chtit pb qd même 
Merci pour l'aide :
Exercice1)
Soit E un espace vectoriel de dimension 3 rapporté à une base (  ,
,  ,
, )
)
Soit a un réel quelconque et A la matrice
A = 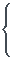 a-2 1 1
a-2 1 1
1 a-2 1
1 1 a-2
1- Pour quelle valeur de a la matrice A est t elle non inversible ?
2- Soient les vecteurs X et B de composants :
X= (x,y,z)
B= (0,3,-3)
On considére le système écrit matriciellement: AX=B
a) résoudre ce système qd le cas où a =0
b) résoudre ce système qd le cas où a= 3
c) pour a =1, calculer A-1 (-1 est en l'air) ; matrice de A et résoudre le système obtenu.
Si je me trompe pas je dois calculer les déterminants et utiliser la méthode dite du Pivot de Gass ?
Pour le 2a) je trouve dét=-4
Pour le 2b) j'ai pas encore calculé.
Exercice2)
La je comprends rien du tout.. 
Soient les matrices à 3 lignes 3 colonnes
A= a 1 1
1 a 1
1 1 a
B= b 1 1
1 b 1
1 1 b
Existe t il des couples (a;b) de nombres réels tels que les matrices A et B soient l'inverses l'une de l'autre ?
Merci beaucoup
Nathalie 
Bonjour Nath63,
1. Tu calcules le déterminant de la matrice en fonction de a.Tu dois obtenir un polynôme de degré 3 en a mais pas de soucis puisque rien qu'à la vue de la matrice on voit qu'il est factorisable par a donc cela donne a fois un polynôme de degré 2 donc la factorisation en polynôme de degré 1 ne devrait pas poser de problème.
A est non inversible <--> detA=0
2.a. Dans ce cas on ne peut utiliser l'inverse de la matrice A puisqu'elle n'est pas inversible  donc il faut faire cela à la main c'est pas très difficile.
donc il faut faire cela à la main c'est pas très difficile.
ce qui donne : x=z-1 et y=z-2 z qcq si je ne me suis pas planté.(x,y,z)=z(1;1;1)+(-1;-2;0)
2b.Là encore pas de bol A n'est pas inversible donc on fait çà à la main on obtient x+y+z=0.
(x,y,z)=x(1;0;-1)+y(0;1;-1)
2c.Pour a=1 il y a plusieurs façons de calculer la matrice inverse soit à la main on inverse le système soit A-1=(comatA)t
| 0 1 1 |
A-1= | 1 0 1 |
| 1 1 0 |
Et donc pour trouver la solution il suffit de caluler A-1b=x
Pour l'exo 2 :
AB=BA=I ou I matrice identité de M3(R)
tu fais les produits matriciels et en égalisant terme à terme avec les coefficients de I cela va te donner des conditions sur a et b (je l'ai pas fait donc pas de réponse à te proposer  )
)
Salut 
Bonjour 
Merci Dad97 pour ta réponse, je vais essayer d'en faire un peu plus mais je crois qu'il faudra que je redemande de l'aide car les matrices et moua c'est dur dure 
A bientôt
Nathalie 
Bonjour 
Suite à la réponse de Dad97, j'ai réfléchi à mes énoncés mais je coince vraiment !!!
Quelqu'un peut t il m'aider un peu plus , suis désolée 

A+ et Merci..
Nathalie 
Rebonjour,
Allons-y :
1.
(explications en dessous)
|a-2 1 1 | (1) | 1 1 1 |
det(A)=| 1 a-2 1 | = a | 1 a-2 1 |
|1 1 a-2| | 1 1 a-2 |
(2) | 1 0 1 |
= a | 1 a-3 1 | = a(a-3)[(a-2)-1]=a(a-3)²
| 1 0 a-2 |
(1) J'additionne toutes les colonnes et je met le résultat dans la première colonne qui devient une colonne avec que des a donc je factorise le déterminant par a pour obtenir que des 1.
(2) je retranche la première colonne à la deuxième colonne et je met le résultat dans la deuxième colonne. Ce qui me permet de développer mon déterminant à partir du terme central.
donc det(A)=a(a-3)²
donc A non inversible <--> a=0 ou a=3 (oh comme c'est bizarre ce sont les valeurs que l'on retrouve plus loin dans l'exercice  )
)
2.a on est dans un cas où A n'est pas inversible donc on fait ça à la main :
on doit donc résoudre :
-2x+y+z=0
x-2y+z=3
x+y-2z=-3
soit :
z=2x-y
x-2y+2x-y=3 (on remplace z par 2x-y)
x+y-4x+2y=-3 (on remplace z par 2x-y)
soit :
z=2x-y
x-y=1 (on réduit et on divise tout par 3)
x-y=1 (on réduit et on divise tout par -3)
soit :
z=2x-y=x+1 (on remplace y par x-1)
y=x-1
et donc l'ensemble des solutions de ce système est :
{x(1,1,1)+(0,-1,1)|x réel}
2b. Oups boulette dans le premier post 
Là encore on est dans un cas où A n'est pas inversible donc on fait à la main :
x+y+z=0
x+y+z=3
x+y+z=-3
ce système n'a pas de solution.
2c.
Inversons la matrice :
A(x,y,z)t=(x',y',z') s'écrit :
-x+y+z=x'
x-y+z=y'
x+y-z=z'
soit :
x=y+z-x'
y+z-x'-y+z=y' (on remplace x par son expression)
y+z-x'+y-z=z'
soit :
x=y+z-x'
z=
y=
soit :
x=
z=
y=
soit :
x=
y=
z=
d'où
(0 1 1)
=
1 0 1)
(1 1 0)
La suite bientôt.
Salut 
Exercice 2 :
Si A et B sont l'inverse l'une de l'autre alors AB=I et BA=I où I est la matrice idendité.
AB=(ab+2 a+b+1 a+b+1)
(a+b+1 ab+2 a+b+1)
(a+b+1 a+b+1 ab+2 )
ce qui nous donne en identifiant aux coefficents de I :
ab+2=1
a+b+1=0
soit :
ab=-1
b=-1-a
soit :
a(-1-a)=-1
b=-1-a
soit :
a²+a+1=0
b=-1-a
or le polynôme du second degré en a de la première équation est de discriminant négatif donc il n'y a pas de réel a qui vérifie cette équation.
Donc il n'existe pas de couples (a;b) de nombres réels tels que les matrices A et B soient l'inverses l'une de l'autre.
Salut 
Bonsoir Dad97 
Merci pour ton aide et ta réponse 
A bientôt
Nathalie 
Bonjour Victor 
Je m'excuse de te déranger mais après lecture et reflexion sur ta réponse, je coince sur certains points 
Voilà mes questions:
Exercice1)
1/1. Pour le calcul du Det(A) avec 1) & 2), je comprends pas en fait comment tu fais car c'est a-2 qui me bloque pour les calculs.
On peut pas calculer le déterminant + simplement ? !
2a/ Ensemble des solutions:
{x(1.1.1)+(0.-1.1)|x réel}
Peut tu m'expliquer car je comprends pour (1.1.1) mais pas pour la suite. 
2c)
Pourquoi tu écris => z=1/2(x'+y') et y=1/2(x'+z')
Comment fait tu pour obtenir la valeur 1/2 ?
Aussi qd tu fais A-1=1/2 1/2 est bien le déterminant et donc il faut pour obtenir la matrice que tu indiques il faut prendre chaque valeur et les multipliées par 1/2 non ?
Si j'ai un peu compris mon cours, est il possible qu'en partant de la dernière matrice on peut remonter à la matrice identité du début ?
Exercice2)
Pour le calcul des produits de matrices, l'ordre a t il une importance ?
Par exemple, a+b+1 moi je trouve pour le même calcul b+a+1...
Je comprends pas trop la fin des tes calculs à partir des indentifiants de I ...


Je te remercie bcp de ton aide et de ta patience Victor 
A bientôt
euh moi c'est pas Victor 
Tu peux calculer le fdéterminant d'une autre manière, la manière "brutausore" celle pour laquelle tu n'est pas sûr, en général, de factoriser ton déterminant :
Je développe par rapport à la première colonne :
det(A)=(a-2)|a-2 1 | - |1 1 | + |1 1 |
|1 a-2| |1 a-2| |a-2 1 |
=(a-2)[(a-2)²-1]-[a-2-1]+[1-(a-2)]
=(a-2)(a²-4a+4-1)-a+2+1+1-a+2
=a3-4a²+3a-2a²+8a-6-a+2+1+1-a+2
=a3-6a²+9a
=a(a²-6a+9)=a(a-3)²
Je ne sais pas si c'est plus simple (il y a en tout cas plus de facilité pour se perdre dans les calculs).
La suite bientôt.
Salut 
{x(1.1.1)+(0.-1.1)|x réel} peut s'écrire aussi {(x;x-1;x+1)|x réel} je ne sais pas si c'est plus clair
un exemple : si x=2 alors (2;2-1;2+1)=(2;1;3) appartient à ton ensemble de solution.
Je reprend le passage qui semble être délicat :
soit :
x=y+z-x'
y+z-x'-y+z=y' (on remplace x par son expression)
y+z-x'+y-z=z'
soit :
x=y+z-x'
2z-x'=y' (j'ai simplement réduit l'expression)
2y-x'=z' (j'ai simplement réduit l'expression)
soit :
x=y+z-x'
z= j'ai passé tout les termes en prime du même coté on a alors 2z=x'+y'...
y= j'ai passé tout les termes en prime du même coté on a alors 2y=x'+z'...
Pour ce qui de l'exercice 2
a+b+1=b+a+1 puisque ce sont des calculs dans R où tout est merveilleusement commutatif.
Salut 
Pour l'identification avec I
Deux matrices A et B sont l'une inverse de l'autre ssi AB=BA=I (pas de souci ?)
Deux matrices sont égales si tout leur coefficient à la même place dans lesdeux matrices sont égaux :
Si on A=(Aij) et B=(Bij) alors A=B ssi pout tout i et pour tout j on a Aij=Bij.
Bien là c'est un peut l'idée de la démo :
On calcule la matrice AB et on veut qu'elle soit égale à I donc on identifie le terme de la première ligne première colonne de AB au terme du la première ligne première colonne de I et de la même manière on fait cela pour toutes les lignes et pour toutes les colonnes.
Bonsoir Dad97 
Excuse moi d'avoir confondu mais hier j'ai fais des échanges de posts avec Victor 
Pour le déterminant, en effet, c'est plus compliqué car on peut se tromper dans les calculs mais je vais réfléchir aux 2 méthodes.
En fait, qd tu as fais le développement de ton calcul pour le 1/2, bah j'avais trouvé comme toi mais gt pas sur 
J'ai compris oui pour AB=BA=I 
Juste une dernière question,en parralèle j'ai demandé de l'aide à mon prof et il m'a dit que pour la résolution des équations fallait passer par la méthode du Pivot de Gauss avec les inconnues x;y;z.
Peux tu m'expliquer les grandes lignes car je comprends le but de cette méthode mais j'ai du mal qd il faut passer par exemple de L1 à L2 etc..
Encore merci pour ton aide et pour tout 
A bientôt


 algèbre en Bts
algèbre en Bts