Inscription / Connexion Nouveau Sujet
Les representations graphiques.
Bonjour.
En maths on a dû étudier une fonction f(x)= sin(x)/x sauf qu'on avait pas le droit ni d'écrire sa dérivée, pas de calculatrice. On nous conseillait juste de se baser sur nos connaissance à propos de la représentation graphique de sinus et de la fonction inverse.
Au départ je partais plutôt bien puisque j'avais en tête ces deux représentation graphique mais ensuite impossible d'imaginer la représentation graphique de ces deux fonctions à la fois. Je n'allais pas inventer.
Et du coup sans la représentation graphique je n'arrivais pas à répondre aux questions du genre " Est-ce qu'il y a au moins un point d'inflexion" "Une portion concave ?" etc
On a corrigé mais sans expliquer comment trouver la représentation graphique de tête...
Est-ce-qu'il y a une méthode ? 
Bonjour ,
les zéros de sin(x)/x sont les mêmes que ceux de sin(x), x = k*pi à l'exception de x = 0.
entre ces zéros on a des des "arches" qui "ressemblent" à des arches de sinusoïdes déformées, avec un maximum ou un minimum quelque part entre les zéros, mais va savoir où exactement, en tout cas ces extrémas existent et ça nous suffit. (par continuité de f(x) et de sa dérivée sans avoir besoin de la calculer explicitement : f(x) est infiniment dérivable partout sauf en 0, et ça suffit)
reste à "deviner" ce qui se passe dans ]0, pi[ ...
on "sait" que la limite de sin(x)/x quand x tend vers 0 est 1, ça nous donne un point (limite)
et que sin(pi) = 0 (donc sin(pi)/pi aussi !)
mais entre les deux ?? bof...
en tout cas les arches pour x > pi sont suffisemment "explicites" pour répondre à la question posée.
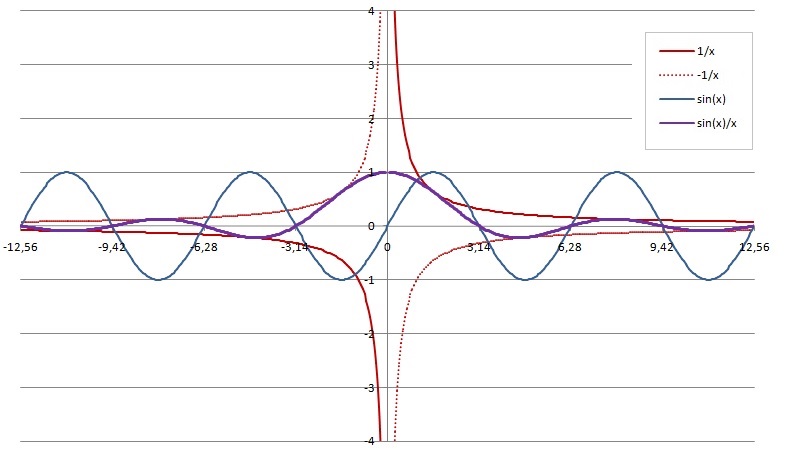
En image, pour "voir" ce qui se passe...
La courbe de f(x) "oscille" avec la même période que sin(x).
Mais son "amplitude" est encadrée par la fonction |1/x|.
Son comportement en 0 doit être étudié par un calcul de limite (confère mathafou)
Bonjour,
Le domaine de définition de la fonction est R* mais il te faudra étudier les limites de f à gauche et à droite de 0.
sin est une fonction impaire
1/x est une fonction impaire
qu'en est-il de f ? f(-x)=sin(-x)/(-x) = -sin(x)/(-x)= sin(x)/x = f(x) donc f est paire càd sa représentation est symétrique par rapport à l'axe des y.
tu connais le graphique de sin(x) qui oscille entre [-1,1] et le graphique de 1/x
La fonction étant paire regardons ce qui se passe sur ]0,+inf[.
Plus x augmente et plus le rapport sin(x)/x devient petite. La sinusoide va s'écraser progressivement pour se rapprocher de 0.
Par symétrie, idem de ]0, -inf[.
Reste à étudier la limite de f en 0+ et 0-.
Le résultat est 1. donc f est telle que f(x)=sin(x)/x sur R* et f(0)=1.
et f(0)=1.
f(x) = sin(x)/x sur R*
en une autre fonction définie sur R tout entier "par morceaux" :
{ g(x) = f(x) pour x
 0
0
{ et g(0) = 1
___
on peut même être plus précis sur l'encadrement de sin(x)/x que "La sinusoide va s'écraser progressivement", en accord avec le graphique de LeDino
comme 0
 |sin(x)|
|sin(x)|  1 sur R tout entier
1 sur R tout entier
on a 0
 |f(x)|
|f(x)|  |1/x| sur tout R*
|1/x| sur tout R*
et donc l'encadrement entre les deux courbes y = 1/x et y = -1/x :
-1/|x|
 f(x)
f(x)  1/|x| sur R*
1/|x| sur R*


