Inscription / Connexion Nouveau Sujet
Limite de fonction
Voici mon énoncé :
Soit f la fonction définie par f(x)=x+ racine carré de (x²-1)
on note cf sa courbe représentative dans un repère.
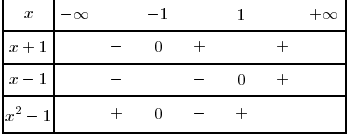
Il me faut tout d'abord déterminer l'ensemble de définition D de f
Est-ce : R+???
oui c'est bien cela!
je suis d'accord avec votre tableau, mais comment ptrouve t'on que
f(x) x f(-x) = -1 ? je ne vois pas le lien...
d'accord je comprend mieux! je ne voyez pas ou voulez en venir!
dans ce cas avec votre tableau, je ne comprend pas...
on proue donc qu epout tout x de D, c'est à dire x égal ou plus grand à 1, on a le produit des deux fonctions positif! OK mais quel rapport avec le fait que cela est égal à -1?
la première question était l'ensemble de définition de
l'ensemble de définition est par conséquent
cela permet d'affirmer que si alors
et le calcul
a un sens
absolument pas or dans
la racine carrée d'un nombre négatif n'est pas définie
si vous êtes d'accord avec le tableau la fonction n'est pas définie entre -1 et 1 exclus
ah oui! je suis bête, d'accord pour l'ensemble de définition.
Le tableau a donc un sens avec le produit des différentes fonctions.
Mais on prouve pour tout x qui appartient à D, c'est positif mais c'est pas égal à -1????!!!
f(x) x f(-x) = -1
c'est parce que et
appartiennent à D que l'on peut faire le produit
et on montre ainsi que est l'inverse de l'opposé de
de la forme
d'où calcul à poursuivre
la question d'après je doit déterminer la limite de f en +infini et ensuite en -infinie mais en utilisant la quesiton précédente.
pour x tend vers +infini, je trouve bien que la limite est +infinie
pour x tend vers -infini, la limite est O par limite d'un quotient en levant l'indetermination.
MAIS JE NAIS PAS UTILISER COMME LA CONSIGNE LE VEUT LA QUESTION PRECEDENTE! le fait que f(x) x f(-x) = -1
comment l'exploiter???????