Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Partager :

Limite : théorème de composition

Posté par
hbx360 07-12-18 à 13:25

Bonjour,

Pourriez-vous me dire si la définition graphique du théorème de composition que j'ai fait est correct. Ce qui me gène c'est pour placer le L et l'inclusion entre les 2 intervalles. Merci.

Def. : Proposition 6.3.1. Soient :
f : I \rightarrow R,  g : J \rightarrow R,
a  \epsilon  I ( ou a = +oo ou a = -oo éventuellement),
b  \epsilon  J ( ou b = +oo ou b = -oo éventuellement).
On suppose que f(I) \subset J.

Alors \lim_{x \rightarrow a}f(x) = b, et

\lim_{y \rightarrow b} g(y) = l \Rightarrow \lim_{x \rightarrow a }(g o f)(x) = l.

Déf. graphique :

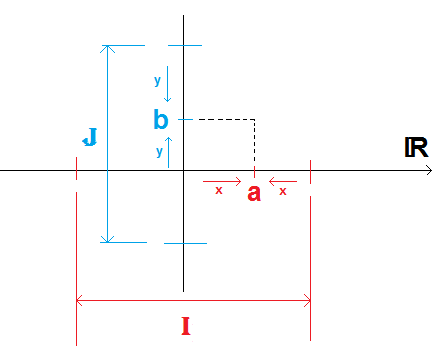
Limite : théorème de composition

Posté par
Camélia Correcteurre : Limite : théorème de composition 07-12-18 à 14:33

Bonjour

D'abord ton écriture n'est pas correcte. La conclusion est

{\red (}\lim_{x \rightarrow a}f(x) = b \ et \ \lim_{y \rightarrow b} g(y) = l {\red )}\Rightarrow \lim_{x \rightarrow a }(g o f)(x) = l


Par ailleurs ton dessin est correct, mais on n'y voit pas grand chose! En particulier g\circ f n'apparait nulle part. Peut-être qu'avec des graphes des fonctions se serait plus clair, mais je ne vois pas l'intérêt!

Posté par
hbx360re : Limite : théorème de composition 07-12-18 à 16:00

Merci pour ton message.
En fait la proposition vient d'un poly fait par un prof universitaire, mais ce que je trouve dommage c'est que dans son poly pour cette proposition il n'y a pas de graphe de fonctions.
'intérêt pour moi et que cela me permettrai de pouvoir bien comprendre par le graphique la proposition énoncé, c'est pour ça que je demandais.

Merci encore.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !