le graphe de la fonction y=x² est loin d'être celui d'une droite, non ?

Bonjour,
Houlàlàlà !
Une courbe d'une droite


une droite  peut se partager en 2 groupes :
1)y=ax+b. (avec peut être b=0); ou encore y=B

l'autre groupe sont les droites du types 2) x=c.
tout ce qui n'est pas de ce type n'est pas une droite.

(on admet que tu n'as pas encore vu les équation cartésiennes de droites)

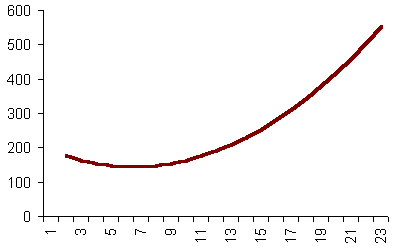
Je sais pas comment expliquer, j'ai un graphique ou la droite est une courbe....

Ca ressemble un peu à ca
http://www.peoi.org/Courses/Coursesfr/mic/Resources/Image331.gif

Mais je ne sais pas comment définir une fonction à partir de ça.

UP !

Personne pour m'aider ?

il te faut définir une fonction y=f(x) dont le graphe est "proche" de la courbe réelle.

la courbe réelle doit te faire penser à une parabole (d'axe de symétrie verticale)
(c'est un cas simple, mais dans tes études, tu ne risques pas d'en voir de beaucoup plus compliqués)

tu dois savoir qu'une telle parabole a une équation générale de la forme
y=ax²+bx+c

reste à définir quelques caractéristiques de ta courbe réelle et les imposer à ta parabole

ta courbe réelle semble :
passer par le point (2;180)
passer par le point (7;120) et y avoir son sommet.

en partant de là, on a les équations suivantes qui vont nous permettre de calculer a, b et c

passer par le point (2;180) :
190 = a*2² + b*2 + c
passer par le point (7;120) :
120 = a*7² + b*7 + c
y avoir son sommet (j'utilise une propriété de la parabole qui dit que si S(x;y) est le sommet de la parabole, alors 2ax = -b, mais tu peux aussi te servir du fait que la dérivée sera nulle, puisque la tangente sera horizontale)
2a*7 = -b
la résolution du système suivant
190 =  4a + 2b + c
120 = 49a + 7b + c
0   = 14a +  b
donne la solution :
a=12/5 ; b=168/5 ; c= 1188/5

ta courbe


le résultat


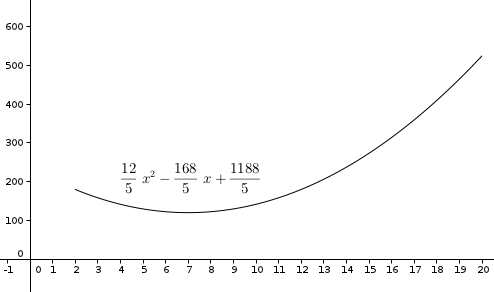
pas très bon, elle monte trop vite, on doit pouvoir améliorer en jouant sur les coefficients

Ma courbe n'a pas les mêmes valeurs que l'exemple que j'ai montré.
Et la méthode que tu as fait je ne l'ai jamais vu en cours...

Y'a pas une méthode "facile" ?

mais merci quand même.

donne donc alors le plus précisément possible l'énoncé exact, sinon on risque de tourner pas mal de temps en rond.