Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Prepa intégrée ProbabilitésTopics traitant de probabilités [tout]Lister tous les topics de mathématiques
Niveau Prepa intégrée
Partager :

Loi et covariance.

Posté par
matheux14 29-01-23 à 17:44

Bonsoir,

Merci d'avance.

X et Y sont deux v.a.

La densité du couple (X, Y) est :

f(x, y) = \begin{cases} k \exp(-(x + y)) \text{ si } 0 \le x \le y \\\\ 0 ~~~~~~~~~~~~~~~~~~~~\text{ sinon } \end{cases}

1) Trouver k.

2) Calculer les lois marginales de X et Y.

3) X et Y sont-elles indépendantes ?

4) Quelle est la covariance Cov(X, Y) de X et Y ?

5) Soit le couple (Z, U) avec Z = X + Y et U = Y.

a) Prouver que le support du couple (Z, U) est :

\Delta = \left\{(z, u) \in \R_+ \times \R_+ : \dfrac{z}{2} \le u \le z\right\}.

b) Calculer la loi du couple (Z, U).

c) Déduire alors la loi de Z.


Réponses

1) Pour trouver k, j'ai intégré la fonction f(x, y) sur son domaine de définition. On a donc :

\int_{0}^{\infty}\int_{0}^{y} k \exp(-(x + y)) dxdy = 1

L'intégration donne :

k \int_{0}^{\infty} \exp(-y)\left(\int_{0}^{y} \exp(-x) dx \right)dy = k \int_{0}^{\infty} \exp(-y)\dfrac{1 - \exp(-y)}{-1}dy = k \int_{0}^{\infty} \exp(-y)dy - k \int_{0}^{\infty} \exp(-2y)dy = 1

On peut alors résoudre pour k :

k = \dfrac{1}{\int_{0}^{\infty} \exp(-y)dy - \int_{0}^{\infty} \exp(-2y)dy} = \dfrac{1}{\dfrac{1}{1} - \dfrac{1}{2}} = 2

2) Les lois marginales de X et Y peuvent être trouvées en intégrant la fonction f(x, y) sur l'ensemble approprié :
f_X(x) = \int_{0}^{\infty} k \exp(-(x + y)) dy = 2 \exp(-x)\left(\int_{x}^{\infty} \exp(-y)dy\right) = 2 \exp(-x)\left(\dfrac{1}{\exp(-x)}\right) = 2

f_Y(y) = \int_{0}^{y} k \exp(-(x + y)) dx = 2 \exp(-y)\left(\int_{0}^{y} \exp(-x) dx \right) = 2 \exp(-y)\dfrac{1 - \exp(-y)}{-1} = 2(1 - \exp(-y))

Posté par
verdurinre : Loi et covariance. 29-01-23 à 18:40

Bonsoir,
on doit avoir \int_0^{+\infty}f_X(x)dx=1

Posté par
matheux14re : Loi et covariance. 29-01-23 à 19:28

Ah oui,

La fonction de densité marginal de X est donnée par :

f_X(x) = \int_{-\infty}^{+\infty} f(x, y) dy

En effectuant l'intégration sur l'intervalle 0 \le x \le y :

f_X(x) = k \int_{x}^{+\infty} \exp(-(x + y)) dy

En utilisant la substitution u = x + y, on a :

du = dy, et donc dy = du.

f_X(x) = k \int_{x}^{+\infty} \exp(-u) du = -k \exp(-u) \big|_{u = x}^{u = +\infty} = k \exp(-x).

Donc, k = 1, et f_X(x)=e^{-x}.

Posté par
matheux14re : Loi et covariance. 29-01-23 à 19:32

On peut trouver la densité de Y, f_Y(y), en utilisant la formule de l'espérance :

f_Y(y) = \int_{-\infty}^\infty f(x,y)dx

En utilisant la définition de f(x,y), on a :

f_Y(y) = \int_0^y k \exp(-(x+y))dx

En effectuant l'intégration, on obtient :

f_Y(y) = k \exp(-2y)

Donc, la densité de Y est une loi exponentielle de paramètre \lambda = 2.

f_Y(y) = e^{-2y}

Posté par
verdurinre : Loi et covariance. 29-01-23 à 19:47

Non.
Je pose D=\{(x,y)\in\R^2\; |\; 0\le x\le y\}

f_X(x)=\int_\R 2\exp(-(x + y)) \cdot\mathbf{1}_D(x,y)dy=\int_x^{+\infty}2\exp(-(x + y)) dy

Tu ne peux pas changer la densité du couple (X,Y).

Posté par
matheux14re : Loi et covariance. 29-01-23 à 19:58

Du coup on utilise la formule de l'intégration par rapport à y :

f_X(x)=\int_x^{+\infty}2\exp(-(x + y)) dy = 2 \exp(-x) \int_0^{+\infty} \exp(-y) dy

= 2 \cdot \left( - \exp(-(x+y)) \right)\big|_x^{+\infty}

= 2 \cdot \left( - \exp(-x) + \lim\limits_{y \to \infty} \exp(-(x+y)) \right)

= 2 \cdot \left( - \exp(-x) \right)

f_X(x)= 2e^{-x}

Posté par
matheux14re : Loi et covariance. 29-01-23 à 20:05

En procédant de façon analogique, je trouve f_Y(y)=2e^{-2y}(1 - y)

Posté par
verdurinre : Loi et covariance. 29-01-23 à 20:40

\begin{aligned}f_X(x)=\int_x^{+\infty}2\exp(-(x + y)) dy = 2 \exp(-x) \int_{{\color{red}x}}^{+\infty} \exp(-y) dy\end{aligned}.

Posté par
matheux14re : Loi et covariance. 29-01-23 à 20:49

Donc f_X(x) =  2 e^{-2x}.

Posté par
verdurinre : Loi et covariance. 29-01-23 à 20:52

Et \int_x}^{+\infty} \exp(-y) dy = ?

Posté par
verdurinre : Loi et covariance. 29-01-23 à 20:55

Oui, c'est bien ça.
Recalcule soigneusement f_y(y) et ne tiens pas compte de mon message précédent.

Posté par
matheux14re : Loi et covariance. 29-01-23 à 20:56

\int_x}^{+\infty} \exp(-y) dy = 1 -e^{-x}

Posté par
matheux14re : Loi et covariance. 29-01-23 à 21:09

On a f_Y(y)=\int_{-\infty}^{y}2\exp(-(x + y)) dx. En intégrant, on obtient :

\begin{aligned}f_Y(y) &= 2\exp(-y)\left(\int_{-\infty}^{y} \exp(-x) dx\right) \ &= 2\exp(-y)\left(\int_{-\infty}^{0} \exp(-x) dx + \int_{0}^{y} \exp(-x) dx\right) \ &= 2\exp(-y)\left(-\exp(0) + \exp(-y)\right) \ &= 2\exp(-2y)\end{aligned}.

f_Y(y) = 2e^{-2y}

Posté par
matheux14re : Loi et covariance. 29-01-23 à 21:21

3) Pour savoir si deux variables aléatoires X et Y sont indépendantes, il faut vérifier si leur densité conjointe est égale au produit de leurs densités marginales. Si c'est le cas, alors X et Y sont indépendantes, sinon, elles ne le sont pas.

Dans ce cas précis, la densité conjointe est donnée par :

f_{X,Y}(x,y) = \exp(-(x + y)) \mathbf{1}_D(x,y)

Où D est le domaine défini par 0 \le x \le y.

La densité marginale de X est :

\begin{aligned}f_X(x) = \int_{-\infty}^{+\infty} \exp(-(x + y)) \mathbf{1}_D(x,y) dy = 2e^{-x}\end{aligned}

La densité marginale de Y est :

\begin{aligned}f_Y(y) = \int_{-\infty}^{+\infty} \exp(-(x + y)) \mathbf{1}_D(x,y) dx = 2e^{-y}\end{aligned}

Comme on peut le voir, f_{X,Y}(x,y) = \exp(-(x + y)) \mathbf{1}_D(x,y)  \neq f_X(x)f_Y(y) = 4e^{-(x + y)}, donc X et Y ne sont pas indépendantes.

Posté par
matheux14re : Loi et covariance. 29-01-23 à 21:31

J'ai oublié un 2 au niveau de l'expression de f_{X,Y}(x,y) = {\red{2}} \exp(-(x + y)) \mathbf{1}_D(x,y)  \neq f_X(x)f_Y(y) = 4e^{-(x + y)}, donc X et Y ne sont pas indépendantes.

4) Pour trouver la covariance de X et Y, on peut utiliser la formule :
Cov(X, Y) = E((X - E(X))(Y - E(Y)))

D'abord, on trouve les espérances de X et Y :

E(X) = \int_{0}^{\infty} \int_{0}^{y} x k e^{-(x+y)} dxdy = \dfrac{k}{2}

E(Y) = \int_{0}^{\infty} \int_{0}^{y} y k e^{-(x+y)} dxdy = \dfrac{3k}{2}

Ensuite, on peut trouver la covariance :

Cov(X, Y) = E((X - E(X))(Y - E(Y)))

= \int_{0}^{\infty} \int_{0}^{y} \left(x - \dfrac{k}{2}\right) \left(y - \dfrac{3k}{2}\right) k e^{-(x+y)} dxdy

= \dfrac{k}{2}\left(\dfrac{3k}{2} - \dfrac{k}{2}\right)

= \dfrac{3k^2}{4}

Posté par
matheux14re : Loi et covariance. 29-01-23 à 21:39

Or k = 2, du coup Cov(X, Y) = 3

Posté par
matheux14re : Loi et covariance. 29-01-23 à 21:44

5-a) La transformation du couple (X, Y) vers (Z, U) est définie par :

Z = X + Y et U = Y

Donc Z = U + X.

X = Z - U

Il est clair que X \ge 0 et Y \ge 0.

De plus, pour que le couple (X, Y) soit dans le support de la densité f(x, y), on doit avoir 0 \le X \le Y.

En remplaçant X par Z - U et en utilisant les propriétés de l'égalité, on trouve que :

0 \le Z - U \le U.

D'où, pour que le couple (Z, U) soit dans le support de la densité, on doit avoir \dfrac{Z}{2} \le U \le Z.

b) On doit calculer la loi du couple (Z, U).

Nous allons utiliser la transformation de variables, en utilisant la relation suivante :

f_{Z,U}(z,u) = f_{X,Y}(x,y) \left|\frac{\partial(x, y)}{\partial(z, u)}\right|

où \left|\frac{\partial(x, y)}{\partial(z, u)}\right| est le déterminant de la matrice Jacobienne.

On a déjà trouvé que le support du couple (Z, U) est \Delta = \left\{(z, u) \in \R_+ \times \R_+ : \frac{z}{2} \le u \le z\right\}.

Maintenant, nous allons déterminer la transformation de variables. Si (z, u) \in \Delta, alors x = z - u et y = u. En remplaçant ces valeurs dans la fonction de densité de (X, Y), nous obtenons :

f_{Z,U}(z,u) = f_{X,Y}(z-u,u) = k \exp(-(z - u + u)) = k \exp(-z)

Le déterminant de la matrice Jacobienne est alors égal à 1, car la transformation est une translation.

Finalement, la loi du couple (Z, U) est :

f_{Z,U}(z,u) = k \exp(-z)$ pour $(z, u) \in \Delta

f_{Z,U}(z,u) = 0$ pour $(z, u) \notin \Delta

Posté par
verdurinre : Loi et covariance. 29-01-23 à 21:59

Citation :
La densité marginale de Y est :

\begin{aligned}f_Y(y) = \int_{-\infty}^{+\infty} \exp(-(x + y)) \mathbf{1}_D(x,y) dx = 2e^{-y}\end{aligned}
NON
\begin{aligned}f_Y(y) = \int_{-\infty}^{+\infty} {\color{red}2}\exp(-(x + y)) \mathbf{1}_D(x,y) dx =\int_0^y 2\exp(-(x + y))dx=2\exp(-y)\int_0^y\exp(-x)dx\end{aligned}

Le fait que X et Y ne sont pas indépendantes est évident car on a XY par hypothèse.

Je n'ai pas encore lu ton dernier message.

Posté par
matheux14re : Loi et covariance. 29-01-23 à 22:04

Oui j'ai oublié le 2 en saisissant.

Ça ne change rien au résultat.

Posté par
matheux14re : Loi et covariance. 29-01-23 à 22:07

5-c) Pour déduire la loi de Z, nous pouvons utiliser la méthode de transformation de variables :

F_Z(z) = P(Z \le z) = P\left(\dfrac{Z}{2} \le U \le Z\right) = \int_{\dfrac{z}{2}}^{z}f_{Z, U}(z, u)du

Où f_{Z, U}(z, u) est la densité de (Z, U).

La Jacobienne de la transformation est :

J(z, u) = \left|\dfrac{\partial(x, y)}{\partial(z, u)}\right| = \frac{1}{2}

Donc :

f_{Z, U}(z, u) = f_{X, Y}(x, y)\left|\dfrac{\partial(x, y)}{\partial(z, u)}\right| = \dfrac{1}{2}k\exp(-x-y)

On remplace x et y en fonction de z et u :

x = \dfrac{z-u}{2}

y = \dfrac{z+u}{2}

f_{Z, U}(z, u) = \frac{1}{2}k\exp\left(-\dfrac{z-u}{2}-\dfrac{z+u}{2}\right) = \dfrac{1}{2}k\exp\left(-z\right)\exp\left(-\dfrac{u}{2}\right)

Intégrons sur u :

F_Z(z) = \int_{\dfrac{z}{2}}^{z} \dfrac{1}{2}k\exp\left(-z\right)\exp\left(-\dfrac{u}{2}\right) du = \dfrac{1}{2}k\exp\left(-z\right)\int_{\dfrac{z}{2}}^{z} \exp\left(-\dfrac{u}{2}\right) du

La dérivée de l'intégrale est :

f_Z(z) = \dfrac{d}{dz}F_Z(z) = \dfrac{1}{2}k\exp\left(-z\right)\left(\exp\left(-\dfrac{z}{2}\right) - \exp\left(-\dfrac{z}{2}\right)\right) = 0

Donc la loi de Z est une loi constante et la densité est 0.

En conclusion, la loi de Z est une loi uniforme sur [0, +\infty[.

Posté par
verdurinre : Loi et covariance. 29-01-23 à 22:43

Je suis trop fatigué pour lire attentivement tes derniers messages.
Mais la conclusion est absurde.
Il n'y a pas de loi uniforme sur [0, +\infty[.

Bonne nuit.

Posté par
matheux14re : Loi et covariance. 29-01-23 à 22:47

Ok, je revois alors.

Bonne nuit à vous aussi.

Posté par
verdurinre : Loi et covariance. 30-01-23 à 17:36

Je reprend pour les lois marginales avec un petit dessin.
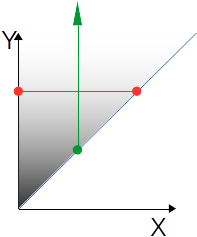
Loi et covariance.
Le support de (X,Y) est en dégradé de gris, on va imaginer que ce gris représente la densité du couple.

En vert on a une ligne X=x, la densité marginale f_X(x) est la quantité de gris sur la ligne d'où
\begin{aligned}f_X(x)=\int_x^{+\infty} 2\mathbf{e}^{-x-y}\text{d}y=2\mathbf{e}^{-x}\end{aligned}

En rouge on a une ligne Y=y, la densité marginale f_Y(y) est la quantité de gris sur la ligne d'où
\begin{aligned}f_Y(y)=\int_0^{y} 2\mathbf{e}^{-x-y}\text{d}x= 2\mathbf{e}^{-y}\int_0^{y} 2\mathbf{e}^{-x}\text{d}x=\ldots\end{aligned}

Ensuite vient le calcul de E(X) et E(Y).
La variable aléatoire X suit une loi exponentielle de paramètre 2 son espérance est donc 1/2. Comme tu ne donnes pas les calculs je ne sait pas où tu t'es trompé.
Personnellement, si je ne connaissais pas le résultat, je calculerais
\begin{aligned}\matsf{E}(X)=\int_0^{+\infty} xf_X(x)\text{d}x=\int_0^{+\infty}2x\,\mathbf{e}^{-2x}\text{d}x=\frac12\end{aligned}

Pour l'espérance de Y :
\begin{aligned}\matsf{E}(Y)=\int_0^{+\infty} yf_Y(y)\text{d}y=\ldots\end{aligned}

Il y a la même erreur de calcul dans les deux cas et vraisemblablement aussi dans le calcul de la covariance.

Posté par
verdurinre : Loi et covariance. 30-01-23 à 17:39

Correction \large f_X(x)=2\mathbf{e}^{-{\color{red}2}x}

Posté par
verdurinre : Loi et covariance. 30-01-23 à 18:13

Autre correction

\begin{aligned}f_Y(y)=\int_0^{y} 2\mathbf{e}^{-x-y}\text{d}x= 2\mathbf{e}^{-y}\int_0^{y} \mathbf{e}^{-x}\text{d}x=\ldots\end{aligned}
Il y avait un 2 en trop dans la seconde intégrale, malheur de ctrlC.

Pour la loi de Z tu as prouvé que :
f_{ZU}(z,u)=\begin{cases}2\,\mathbf{e}^{-z}&\text{si } \frac{z}2\leqslant u\leqslant z\\0&\text{sinon }\end{cases}

On a donc :
\begin{aligned}f_Z(z)=\int_{z/2}^{z} 2\,\mathbf{e}^{-z}\text{d}u=2\,\mathbf{e}^{-z}\int_{z/2}^{z} \text{d}u\end{aligned}

Si tu connais Z suit une loi .


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !