Annuler
connectez vous
probabilités en post-bac
- Un best-of d'exos de probabilités (après le bac)
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Ensemble et application Partie II
- Espaces vectoriels et Applications linéaires - supérieur
- Décomposition des matrices en blocs, exponentielle de matrices - supérieur
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Autre ProbabilitésTopics traitant de probabilités [tout]Lister tous les topics de mathématiques
Niveau autre
loi exponentielle
Posté par romu
Bonjour,
Citation :
Soit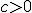
. On dit qu'une variable aléatoire \rightarrow \mathbb{R})
suit la loi exponentielle de paramètre 
(qu'on note )
),
si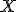
a pour densité (par rapport à la mesure de Lebesgue)
=c \exp(-cx)\mathbb{1}_{\mathbb{R}_+}\qquad \qquad (x\in \mathbb{R}))
.
1. Calculer la fonction de répartition, l'espérance et la variance de.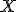
2. On pose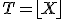
, 
désignant la partie entière inférieure. Quelle est la loi de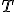 
?
Soit
si
1. Calculer la fonction de répartition, l'espérance et la variance de
2. On pose
Pour la 1. je pense que c'est ok, je trouve
la fonction de répartition
l'espérance
Après pour la 2. je ne vois pas pourquoi
Merci pour votre aide.
Bonjour,
Il me semble que pour n entier, "T = n" 
"n 
X < n+1" . A partir de là tu peux trouver la loi de T ...
ok merci PIL, donc en fait on a pas besoin de savoir que , savoir que
suffit et je pars comme tu dis.
En fait, il me semble que c'est presque une question de goût :
dire que 
= 
et avoir P(T=n) = 0 pour tous les n négatifs, ou dire que = 
.
merci.
Bon donc j'ai trouvé .
Citation :
3. Soit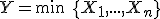
, où 
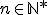et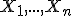 
sont des v.a. indépendantes et de même loi exponentielle de paramètre .
Déterminer la loi de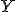
, en déduire l'espérance et la variance de 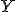, en déduire l'espérance et la variance de .
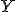3. Soit
Déterminer la loi de
Je trouve que la fonction de répartition de
donc
Je galère sur la dernière question:
Citation :
4. Une v.a.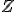
est dite sans mémoire sur 
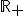si =\mathbb{R}_+)
,
>0,\ \mbox{ et } \forall s,t>0,\ \mathbb{P}^{Z\geq t}(Z>t+s)=\mathbb{P}(Z>s))
.
Montrer qu'il y a équivalence entre:
(i)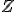 est sans mémoire sur ,
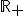(ii)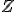 suit la loi exponentielle de paramètre avec ))
.
4. Une v.a.
Montrer qu'il y a équivalence entre:
(i)
(ii)
Déjà pour (i)=>(ii) je bloque.
J'ai posé
je trouve que pour tout
là je ne vois pas comment en déduire que
