Bonsoir, j'ai cet exercice à faire pour la fin de semaine et je n'ai pas beaucoup de temps, j'aurais besoin d'aide s'il vous plait.
Elise et Anthony viennent d'acheter un terrain 𝐴𝐵𝐶𝐷 de forme carrée de côté 8 𝑚.
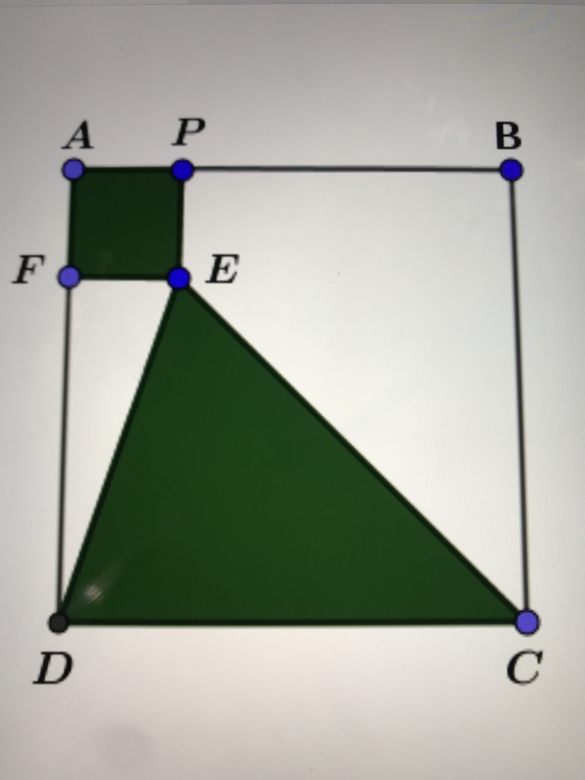
A l'intérieur de ce terrain, ils veulent aménager un jardin. Ce jardin, de forme très originale, est composé d'un carré et d'un triangle ayant un sommet en commun 𝐸 (voir le schéma ci-contre).
Elise se demande où placer le point 𝑃 sur le segment [𝐴𝐵] pour que ce jardin occupe exactement la moitié du terrain.
On note 𝑥 la longueur 𝐴𝑃.
PARTIE A : expression algébrique de l'aire du jardin
1. Entre quelle et quelle valeur 𝑥 varie-t-il ?
2. Exprimer l'aire du carré du jardin 𝐴𝑃𝐸𝐹 en fonction de 𝑥.
3. Exprimer la hauteur du triangle 𝐷𝐸𝐶 issue de 𝐸 du jardin en fonction de 𝑥.
4. Exprimer l'aire du triangle 𝐷𝐸𝐶 du jardin en fonction de 𝑥.
5. A l'aide des questions 2. et 4., montrer que l'aire totale, notée 𝐴(𝑥), du jardin est donnée par
l'expression : 𝐴(𝑥) = 𝑥2 − 4𝑥 + 32.
PARTIE B : Réponse à la question de Elise
1. Développer (𝑥 − 2)2 et en déduire que 𝐴(𝑥) = (𝑥 − 2)2 + 28
2. Expliquer pourquoi, pour répondre à la question de Marie, il suffit de résoudre l'équation 𝐴(𝑥) = 32
3. Résoudre l'équation 𝐴(𝑥) = 32 en utilisant l'expression la plus adaptée de 𝐴(𝑥).
4. Donner la réponse à la question d'Elise.