Inscription / Connexion Nouveau Sujet
matrice inverse
Bonsoir !
J'ai cette matrice à inverser par le pivot de Gauss, ça fait 1semaine que je suis dessus je n'aboutis à rien ! Ou presque
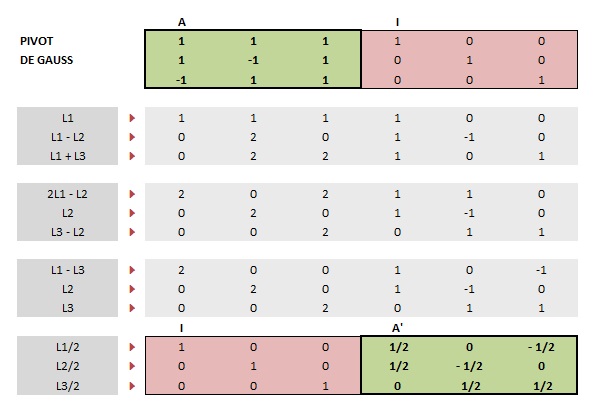
1 1 1
1 -1 1
-1 1 1
J'ai prouvé qu'elle était inversible, j'arrive à :
1 1 0
5 1 0
-1 1 1
Pouvez vous m'aider s'il vous plaît ?????
Merci d'avance !
salut
avec une reduite de gauss j'arrive à
1 1 1
0 -2 0
0 2 2 en ayant effectué L2 <---L2 - L1 et L3 <----L3+L1
1 1 1
0 -2 0
0 0 2 en ayant effectué L3 < --- L3+L2
Merci de cette grande aide !
Je dois de plus déterminer la matrice D telle que A=PDP^-1
Dois-je résoudre ce système ou utiliser les matrices ?
Voici le polynome caractéristique :
det ( A - L I) = - (L-1)(L-1)(L+1) = -L3 + L2 + L - 1
et det (A - L I) = 0
<=> I = -L3 + L2 + L
en remplaçant L par A :
<=> I = -A3 + A2 + A
en multipliant par A-1 :
<=> A-1= -A2 + A + I
voila 
ah ok, en fait pour chaque matrice tu as un polynome qui s'appelle le polynome caracteristique qui s'écrit:
p(L) = det ( A - L I)
L = valeur propre
I = matrice identité (1 sur la diagonale, 0 ailleurs)
det = déterminant de la matrice
normalement tu devrais savoir comment calculer le déterminant d'une matrice sinon regarde ds tes cours ou sur le net. J'ai fait le calcul au dessus pour ta matrice de l'exercice.
Ensuite une des propriétés du polynome caracteristique est que :
p(L) = 0 et aussi p(A) = 0
J'utilise la propriété p(A)=0 au-dessus pour trouver A-1 en fonction des puissances de A
ce qui rend le cacul de A-1 beaucoup plus facile plutot que d'utiliser les pivots etc... 
MERCI beaucoup pour votre réponse, je n'ai pas appris à faire comme cela pour trouver une matrice inverse
Par contre pour trouver la matrice D telle que A=PDP^-1 , savez vous comment faire ?
voici un exemple comment calculer avec les matrices de passage:
http://www.prepacom.net/HEC2/math/cours/Changement%20de%20bases.pdf
il suffit de remplacer les valeurs 
exactement ça oui
ne te laisse pas impressionner par ceux qui veulent te faire le cours de l'an prochain déjà maintenant 
Huggy, honnêtement, trouver plus facile de calculer un déterminant que d'inverser une matrice par la méthode du pivot .... hem ! tu le calcules comment ce déterminant ? avec le même nombre d'opérations, voire moins, la matrice est déjà inversées, par la méthode du pivot.
Ahahah merci ! Donc pour trouver D sous forme matriciel je dois d'abord faire P^-1 * A ou A*P ?? Ou bien autre chose ?
Ou bien autre chose ?
comme tu veux : le produit des matrices est associatif, alors calculer ou
, ça donnera la même chose.
le polynome caractéristique c'est du niveau 1ère année d'études supérieures,
c'est pour cela que j'ai donné cette solution.
mais c'est parfaitement inutile pour inverser une matrice !
et si elle commence seulement l'étude des matrices, elle n'a pas encore parlé de déterminant et encore moins de diagonalisation (qui dans bien des formations est au programme de deuxième année, sans compter que le th de Cayley n'est pas au programme dans tous les cursus)
le produit des matrices est associatif, mais pas commutatif : tu peux déplacer les parenthèses, pas les matrices.
ici tu dois calculer , et D devrait être diagonale, j'imagine (mais comme tu ne nous as pas donné A, on ne peut pas vérifier tes calculs)
On me dit de déterminer la matrice D telle que A=PDP^1 et non telle que A=P^1DP
Donc pourquoi le calculer (si je ne peux pas déplacer les matrices)
Ouf j'ai trouvé ça
Je dois expliciter la matrice A^n définie par A^n=PD^nP^-1
Je trouve une matrice immense, je ne pense pas pouvoir simplifier
Pour le premier terme par exemple, je trouve:
1/2.4^n+1/2.6^n
Est-ce cela ?
et tu multiplies du bon côté par la bonne matrice (P d'un côté, son inverse de l'autre)
chaque terme sera une combinaison linéaire de ,
(que tu peux écrire
si tu préfères) et
, c'est normal.



 algèbre en post-bac
algèbre en post-bac