Inscription / Connexion Nouveau Sujet
Matrice - Problème d'Algèbre linéaire
Bonjour,
Je bloque sur un problème d'algèbre linéaire. On me demande de donner l'expression de la matrice A qui projette orthogonalement un point M (x,y) sur la bissectrice du premier quadrant, puis fait une symétrie par rapport à l'axe des x . J'ai attaché la figure pour aider à se le représenter.
Pour l'instant (et je ne sais pas si c'est comme ça qu'il faut le faire) j'ai cherché la matrice P qui fait changer de repère, puis la matrice B qui projète le point M sur l'axe des X de ce nouveau repère. Ensuite je reviens au repère d'origine par la matrice P-1, et enfin j'ai cherché la matrice C qui effectue la symétrie par rapport à l'axe des abscisses.
Ce qui me donne la matrice A qui effectue toutes ces transformations : A = P
BP-1C
et je trouve que la matrice carrée A =
cos2
-cos.sin
sin.cos -sin2
Mais en essayant d'appliquer cela, je trouve un résultat éronné...
Est-ce que quelqu'un pourrait m'aider s'il vous plait? Merci d'avance!
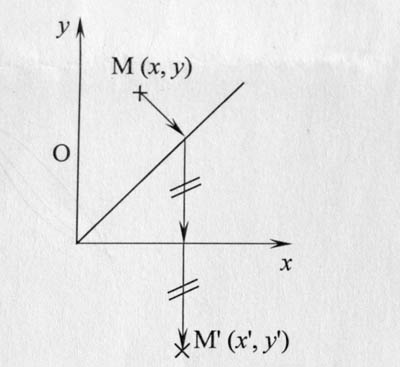
salut
soit M(x,y)
et p la projection orthogonale sur la bissectrice
alors p(M) est le milieu de [M, N] avec N(y,x)
donc p(M) = P((x+y)/,(x+y)/2)) .....
quant à la symétrie d'axe l'axe des abscisses elle est triviale ....
salut
je pense qu'il n'est pas necesssaire de passer par les angles
on peut definir la bissectrice comme l'espace vectioriel E={(x,y)
R²/y-x=0}
et l'espace perpendiculaire à la bissectrice par F={(x,y)R²/ y+x=0}
on prend au depart M ayant pour coordonnées M(x,y) alors le projecté orthogonale de M sur E selon F
est P(x,y))=(xo,yo) comme P(x,y) E alors yo-xo=0 , on a aussi (x,y)-P(x,y) F
donc x-xo+y-yo=0 ce qui donne donc xo=(x+y)/2 et yo=(x+y)/2
donc P(x,y)=((x+y)/2;(x+y)/2) et donc la matrice de la projection de M sur la première bissectrice est
[x']= [1/2 1/2] [x]
[y']= [1/2 1/2] [y]
partant de cette donnée il n'est pas difficile d'ecrire la matrice de la symetrie A (x",y")=A.(x',y')
... allez je termine
(x",y")=(-x',y)
donc [x"] [1 0] [x']
[y"] [0 -1] [y']
donc [x"] [1 0] [x'] [1 0] [1/2 1/2] [x]
[y"] = [0 -1] [y']= [0 -1] x [1/2 1/2] [y]
Annuler
connectez vous
algèbre en post-bac