Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale ArithmétiqueTopics traitant de Arithmétique [tout]Lister tous les topics de mathématiques

1 2 +

Niveau terminale
Partager :

Matrices

Posté par
Krayz 21-04-18 à 23:45

Bonjour,

Petit exercice de révision portant sur les matrices

Citation :
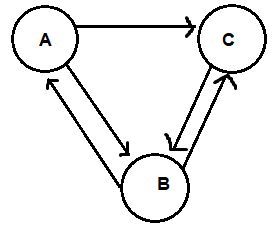
Un réseau comprend trois pages A, B et C.
Les liens sont indiquées dans le graphe.
Un employé navigue de façon aléatoire.
A chaque clic il choisit de façon équiprobable un des liens.
Apres n clics, on note X_n la variable aléatoire donnant la page sur laquelle se trouve l'employé et P_n la matrice ligne (p(X_n=A) p(X_n=B) p(X_n=C)).


Citation :
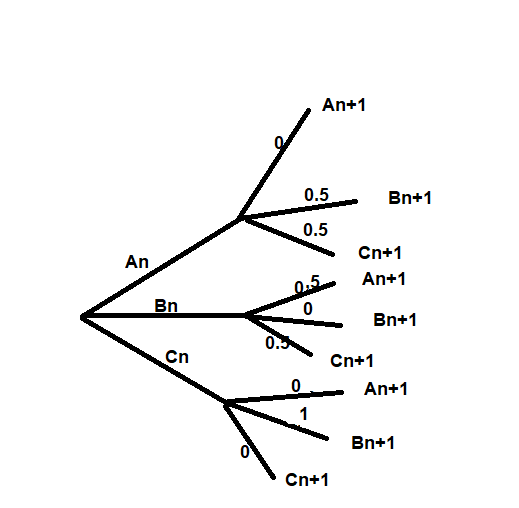
Faire l'arbre.


Matrices

Posté par
Krayzre : Matrices 21-04-18 à 23:46

Données (graphe)

Matrices

Posté par
Krayzre : Matrices 22-04-18 à 00:54

a_{n+1}=p(A_{n+1}) = p(X_{n+1} = A)=0,5b_n
b_{n+1}=p(B_{n+1}) = p(X_{n+1} = B)=0,5a_n+c_n
c_{n+1}=p(C_{n+1}) = p(X_{n+1} = C)=0,5a_n+0,5b_n

(a_{n+1}, b_{n+1}, c_{n+1}) = (a_n, b_n, c_n)*M avec

M = \\ \\ 0 ; 0,5 ; 0,5 \\ 0,5 ; 0; 0,5 \\ 0 ; 1; 0

Posté par
lakere : Matrices 22-04-18 à 08:11

Bonjour,

Oui; mais tu devrais poster l'énoncé complet et ensuite écrire ce que tu as fait.

Posté par
Krayzre : Matrices 22-04-18 à 09:11

Bonjour,

La question était :

1) Ecrire la matrice M telle que P_{n+1}=P_nM, en déduire une relation entre P_n, M et P_0.

Posté par
Krayzre : Matrices 22-04-18 à 09:11

00h54 + P_{n+1}=P_n*M
soit P_n=P_0*M^n

Posté par
lakere : Matrices 22-04-18 à 09:16

Oui mais P_0 dépend de l'état initial; quel est-il? En A, en B ou en C?

Il va falloir calculer M^n

Posté par
Krayzre : Matrices 22-04-18 à 17:36

Pour l'instant ce n'est pas demandé.

Plus loin dans l'exercice oui.
Mais là j'avance seul.

Posté par
Krayzre : Matrices 22-04-18 à 19:02

Citation :
2) a) Soit Q=\begin{pmatrix}1&1&2\\ \\ 1&1&-4\\ \\ 1&-2&4\\ \\ \end{pmatrix}.

Calculer H=Q^{-1}MQ et montrer que H=D+T où D=\begin{pmatrix}1&0&0\\ \\ 0&-0,5&0\\ \\ 0&0&-0,5\\ \\ \end{pmatrix} et T=\begin{pmatrix}0&0&0\\ \\ 0&0&1\\ \\ 0&0&0\\ \\ \end{pmatrix}.


Fait.

Citation :
2) b) Montrer que pour tout n \geq 1 on a D^nT=(-0,5)^nT.


Le mieux est que je fasse le produit matriciel à la main ou que je fasse une récurrence ?

Posté par
Krayzre : Matrices 22-04-18 à 20:31

Définition : Pour tout entier naturel n \ge 1 on note P(n) la propriété définie par « D^nT=(-0,5)^nT ».

Initialisation : pour n = 1, on a : DT=\begin{pmatrix}0&0&0\\ \\ 0&0&-0,5\\ \\ 0&0&0\\ \\ \end{pmatrix}

-0,5T=-0,5\times\begin{pmatrix}0&0&0\\ \\ 0&0&1\\ \\ 0&0&0\\ \\ \end{pmatrix}=\begin{pmatrix}0&0&0\\ \\ 0&0&-0,5\\ \\ 0&0&0\\ \\ \end{pmatrix}

La propriété P(n) est donc initialisée au rang n = 1.

Hérédité :

Supposons que la propriété P(n) définie par « D^nT=(-0,5)^nT » est vraie pour un entier naturel n \ge 1.

Démontrons alors que P(n+1) définie par « D^{n+1}T=(-0,5)^{n+1}T » est également vraie.

D^{n+1}\times T = D^n \times D \times T
D^{n+1}\times T=\begin{pmatrix}1&0&0\\ \\ 0&(-0,5)^n&0\\ \\ 0&0&(-0,5)^n\\ \\ \end{pmatrix}\times \begin{pmatrix}1&0&0\\ \\ 0&-0,5&0\\ \\ 0&0&-0,5\\ \\ \end{pmatrix} \times \begin{pmatrix}0&0&0\\ \\ 0&0&1\\ \\ 0&0&0\\ \\ \end{pmatrix}
D^{n+1}\times T=\begin{pmatrix}1&0&0\\ \\ 0&(-0,5)^{n+1}&0\\ \\ 0&0&(-0,5)^{n+1}\\ \\ \end{pmatrix}\times \begin{pmatrix}0&0&0\\ \\ 0&0&1\\ \\ 0&0&0\\ \\ \end{pmatrix}
D^{n+1}\times T=\begin{pmatrix}0&0&0\\ \\ 0&0&(-0,5)^{n+1}\\ \\ 0&0&0\\ \\ \end{pmatrix}

(-0,5)^{n+1}\timesT=\begin{pmatrix}0&0&0\\ \\ 0&0&(-0,5)^{n+1}\\ \\ 0&0&0\\ \\ \end{pmatrix}

d'où D^{n+1}T=(-0,5)^{n+1}T

La propriété P(n) est donc vraie au rang suivant, elle est donc héréditaire.

Conclusion :

Finalement, le principe de récurrence permet d'affirmer que pour tout entier naturel n \ge 1.

Posté par
lakere : Matrices 22-04-18 à 21:20

Pour moi, c'est trop "lourd".

  Si une matrice D est diagonale:

    D=\begin{pmatrix}a&0&0\\0&b&0\\0&0&c\end{pmatrix}

  il est immédiat que:

     D^n=\begin{pmatrix}a^n&0&0\\0&b^n&0\\0&0&c^n\end{pmatrix}

et le résultat D^nT=(-0.5)^nT s'obtient par un simple calcul de produit de matrices.

Posté par
Krayzre : Matrices 22-04-18 à 21:26

Bonsoir lake,

J'avais eu l'idée de faire un simple calcul matriciel mais j'ai finalement opté pour une récurrence

Je garde donc seulement le corps du calcul de l'hérédité

Posté par
lakere : Matrices 22-04-18 à 21:30

Tu fais comme tu veux; personnellement, je me serais passé de récurrence.

Posté par
lakere : Matrices 22-04-18 à 21:31

et Bonsoir Krayz !

Posté par
Krayzre : Matrices 22-04-18 à 21:33

Citation :
3) Montrer que pour tout n \ge 1 on a H^n=D^n+n(-0,5)^{n-1}T.


Clairement, je pense que la récurrence serait davantage profitable.

Posté par
lakere : Matrices 22-04-18 à 21:36

Je pense aussi

Posté par
Krayzre : Matrices 22-04-18 à 21:52

Initialisation triviale, propriété vraie pour n=1.
Hérédité : Décomposer H^{n+1}=H^nH.

Posté par
lakere : Matrices 22-04-18 à 21:55

Il faut le faire!

Posté par
Krayzre : Matrices 22-04-18 à 22:04

H^{n+1}=H^n \times H
H^{n+1}=(D^n+n(-0,5)^{n-1}T) \times (D+T)

je suis sur la bonne voie ? je dvp ?

Posté par
lakere : Matrices 22-04-18 à 22:11

Mais oui, continue, développe; il y aura des produits matriciels à calculer: T.D et T^2.

Le produit D^n.T est donné dans la question précédente...

Posté par
Krayzre : Matrices 22-04-18 à 22:22

H^{n+1}=H^n \times H
H^{n+1}=(D^n+n(-0,5)^{n-1}T) \times (D+T)

Après calculs,

H^{n+1}=D^{n+1}+n(-0,5)^nT+(-0,5)^nT

Posté par
Krayzre : Matrices 22-04-18 à 22:27

Donc c'est OK si on factorise on retrouve l'expression souhaitée.

Posté par
lakere : Matrices 22-04-18 à 22:27

Tu n'as plus qu'à mettre (-0.5)^n.T en facteur dans les deux derniers termes pour obtenir le n+1

Posté par
Krayzre : Matrices 22-04-18 à 22:45

La grande et dernière question arrive

Posté par
lakere : Matrices 22-04-18 à 22:46

Oh, maintenant, tout est quasiment fait pour le calcul de M^n

Posté par
Krayzre : Matrices 22-04-18 à 23:01

M^n=QH^nQ^{-1}

Posté par
lakere : Matrices 22-04-18 à 23:04

Ben oui et H^n=(D+T)^n que l'on vient de calculer.

Y'a pu qu'à...

Posté par
Krayzre : Matrices 22-04-18 à 23:11

Oui évidemment

Citation :
Exprimer P_n en fonction de n.


P_n=P_0 \times M^n
P_n=P_0 \times (QH^nQ^{-1})
P_n=P_0 \times (Q(D+T)^nQ^{-1})

où P_0=(p(X_0=A) p(X_0=B) p(X_0=C))

Posté par
lakere : Matrices 22-04-18 à 23:15

Oui mais bon; il faut se farcir le calcul de M^n

Posté par
Krayzre : Matrices 22-04-18 à 23:21

lake @ 22-04-2018 à 23:15

Oui mais bon; il faut se farcir le calcul de M^n


Ah ? Il faut dvp° Q(D+T)^nQ^{-1} ?

Posté par
lakere : Matrices 22-04-18 à 23:38

C'est quand même le but de l'exercice:

Obtenir a_n,b_n,c_n (voir tes notations en début de topic à 00h54) en fonction de n.

Tu n'as pas le choix il faut calculer M^n=Q.(D^n+n(-0.5)^n.T).Q^{-1}

Posté par
Krayzre : Matrices 22-04-18 à 23:39

Je l'ai fait depuis tout à l'heure

Posté par
lakere : Matrices 22-04-18 à 23:41

Zut!

M^n=Q.(D^n+n(-0.5)^{n-1}\,T).Q^{-1}

Posté par
lakere : Matrices 22-04-18 à 23:41

Alors tout va bien...

Posté par
Krayzre : Matrices 22-04-18 à 23:44

La seule "chose" qui m'embête dans cet exo° c'est P_0 (état initial).

Posté par
lakere : Matrices 22-04-18 à 23:48

A l'état initial, on est soit en A, soit en B, soit en C qui correspond respectivement aux matrices lignes:

(1 0 0)

(0 1 0)

(0 0 1)

Posté par
Krayzre : Matrices 22-04-18 à 23:52

Il y a équiprobabilité entre (p(X_n=A), p(X_n=B) et p(X_n=C) pour l'état initial donc ?

Posté par
lakere : Matrices 22-04-18 à 23:57

Mais pas du tout! C'est un « état initial » En principe on pourrait le donner dans l'énoncé:

  par exemple: À l'étape 0, on est en B qui correspondrait à P_0=(0\;1\;0)

Posté par
Krayzre : Matrices 22-04-18 à 23:58

P_0 : après 0 clic donc on pourrait être sur n'importe quelle page non ?!

Posté par
lakere : Matrices 23-04-18 à 00:07

C'est à l'énoncé de le définir; au départ, on est soit en A soit en B soit en C.

Ta matrice P_0 est forcément une des trois dont j'ai parlé plus haut.

Dans cet énoncé, on n'en parle pas. Tout ce qu'on peut dire, c'est que:

P_0=(a_0\;b_0\;c_0) avec deux termes nuls et le troisième égal à 1

Posté par
Krayzre : Matrices 23-04-18 à 00:10

lake @ 23-04-2018 à 00:07

C'est à l'énoncé de le définir; au départ, on est soit en A soit en B soit en C.


OK, compris.

lake @ 23-04-2018 à 00:07

Dans cet énoncé, on n'en parle pas. Tout ce qu'on peut dire, c'est que:

P_0=(a_0\;b_0\;c_0) avec deux termes nuls et le troisième égal à 1


Pourquoi a_0=0, b_0=0  et  c_0=1 ?

Posté par
lakere : Matrices 23-04-18 à 00:13

Deux termes nuls parmi les trois. Pas forcément a_0 et b_0

et un terme égal à 1, pas forcément c_0

Ce qui donne les trois matrices lignes initiales possibles.

Posté par
Krayzre : Matrices 23-04-18 à 00:15

Je viens tout juste de comprendre la subtilité (nulle)...

L'énoncé n'indique pas de quelle page nous partons, les trois cas sont possibles en fonction de l'état initial... or, ici on étudie les trois cas...

donc si j'ai compris la suite (P_n) ne dépend pas de l'état initial P_0 !

(facile en réalité)

Posté par
lakere : Matrices 23-04-18 à 00:27

Citation :
or, ici on étudie les trois cas...


Krayz, je te l'ai déjà dit: on n'a pas d'énoncé; tu postes des petits bouts à droite à gauche les trois quart du temps partiels et on ne sait jamais où on va.

Si tu veux qu'on te réponde correctement, il faut que tu postes dès le départ un énoncé complet et exact sans y changer ne serait-ce qu'une virgule.

Ensuite et seulement ensuite, tu postes ce que tu as fait.

Je ne te le redirai pas, c'est toi qui voit...

Bonne nuit

Posté par
Krayzre : Matrices 23-04-18 à 00:29

Bonne nuit lake.

(c'est noté)

Posté par
lakere : Matrices 23-04-18 à 10:04

Pour finir, on obtient:


  M^n=\begin{pmatrix}\dfrac{2}{9}-\dfrac{3n-7}{9}\,(-0.5)^n&\dfrac{4}{9}+\dfrac{3n-4}{9}\,(-0.5)^n&\dfrac{1}{3}-\dfrac{1}{3}\,(-0.5)^n\\\\\dfrac{2}{9}-\dfrac{3n+2}{9}\,(-0.5)^n&\dfrac{4}{9}+\dfrac{3n+5}{9}\,(-0.5)^n&\dfrac{1}{3}-\dfrac{1}{3}\,(-0.5)^n\\\\\dfrac{2}{9}+\dfrac{6n-2}{9}\,(-0.5)^n&\dfrac{4}{9}-\dfrac{6n+4}{9}\,(-0.5)^n&\dfrac{1}{3}+\dfrac{2}{3}\,(-0.5)^n\\\end{pmatrix}

Comme de juste, tu peux vérifier que la somme des termes de chaque ligne vaut 1. Normal pour une matrice de transition.

Lorsque n\to+\infty, la matrice M^n converge vers M_{\infty}=\begin{pmatrix}\dfrac{2}{9}&\dfrac{4}{9}&\dfrac{1}{3}\\\\\dfrac{2}{9}&\dfrac{4}{9}&\dfrac{1}{3}\\\\\dfrac{2}{9}&\dfrac{4}{9}&\dfrac{1}{3}\end{pmatrix}

Et P=\begin{pmatrix}\dfrac{2}{9}&\dfrac{4}{9}&\dfrac{1}{3}\end{pmatrix} est un état stable, c'est à dire qu'on a la relation:

   P.M=P

  que tu peux vérifier.

Posté par
Krayzre : Matrices 23-04-18 à 10:10

C'est ce que j'avais trouvé pour la matrice M^n.

On peut donc conclure qu'à long-terme c'est-à-dire après beaucoup de clics l'utilisateur aura une probabilité d'être sur la page B.

Posté par
lakere : Matrices 23-04-18 à 10:21

Je ne te suis pas trop... Ce qu'on peut dire:

Si P_0=\begin{pmatrix}a_0&b_0&c_0\end{pmatrix} (avec a_0+b_0+c_0=1) caractérise l'état initial, la matrice P_n=\begin{pmatrix}a_n&b_n&c_n\end{pmatrix} converge vers P_0M_{\infty}=\begin{pmatrix}\dfrac{2}{9}&\dfrac{4}{9}&\dfrac{1}{3}\end{pmatrix}

Il suffit de faire le calcul de P_0M_{\infty}

et tu peux te rendre compte qu' à la limite, on atteint cet état stable qui ne dépend pas de l'état initial.

Posté par
Krayzre : Matrices 23-04-18 à 10:24

Oui, ça j'ai compris. D'ailleurs j'avais trouvé P_0M_{\infty}.

Mais la question qui se pose est : « quelle page web sera atteinte avec la plus grande probabilité après un grand nombre de clics ? ».

Posté par
lakere : Matrices 23-04-18 à 10:25

Oui, c'est la B avec une probabilité de \dfrac{4}{9}

1 2 +


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !