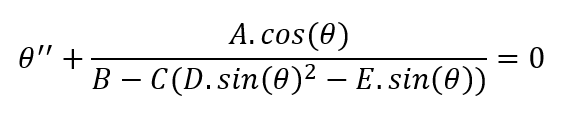
Bonjour,

Quelques questions et remarques.
* Ton objectif est-il d'avoir une solution "d'ingénieur" pour résoudre un problème concret (A, B, C, D, E sont connus), ou de faire des maths ? Dans le premier cas, je te suggère d'utiliser un solveur numérique ; ce n'est pas ce qui manque (voir les toolbox en Python etc...). Ça se règle en quelques lignes de code. Inutile de réinventer la roue.

Sinon, pour l'équation en elle-même, on peut simplifier car il y a trop de constantes (A, B, C, D, E). On pourrait n'en avoir que 3 au lieu de 5 sans perdre la généralité du problème.

Ensuite, la résolution analytique me paraît compliquée si on ne connaît rien des paramètres. Je tenterais deux choses :
1- Si Theta est "petit" alors je linéariserais pour avoir une équation linéaire et je comparerais avec une solution numérique pour voir l'erreur commise selon l'amplitude de Theta.
2- Sinon j'essaierais le changement de fonction y=tan(theta/2) ce qui permet de s'affranchir des cos, sin etc...en utilisant les formules trigos qui vont bien. Mais ce qui ne permettra probablement pas d'en faire plus (à essayer ...).
3- Si l'équation vient d'un système mécanique conservatif, il faut exploiter les invariants ; l'énergie notamment. Voir les méthodes utilisées pour le pendule simple non linéarisé. Ça permet de tirer beaucoup d'informations sur les solution sans pour autant en avoir une expression avec des fonctions usuelles.

Bonne journée

Bonjour,

Merci pour ce retour ! En effet ce que je recherche est une "solution ingénieur, les constantes sont donc considérées connues même si variables (paramètres). Au besoin je peux préciser certaines valeurs, si cela peut aider à la résolution.

J'ai effectivement pensé à une résolution numérique, qui conviendrait parfaitement à mon cas, mais je n'ai pas souvenir d'avoir déjà résolu des équations différentielles du second ordre de cette manière... Je ne sais donc pas trop comment m'y prendre, un lien ou une explication serait bienvenu(e) !

Malheureusement thêta ne peut être considéré comme petit puisque variant entre 0 et 45°. En revanche les 2 derniers points m'interpellent et je vais aller faire quelques recherches de mon côté.

Un grand merci pour ces réponses !

Bonsoir,

En python ça prend quelques lignes. Voici un exemple simple:

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

# Définir l'équation différentielle [y', y''] = f(t, [y, y'])
def f(t, y):
    return [y[1], -2*y[1] - 2*y[0]]

# Conditions initiales
y0 = [1, 0]

# Intervalle de temps
t_span = [0, 10]

# Résolution de l'équation différentielle avec la méthode de Runge-Kutta
sol = solve_ivp(f, t_span, y0, method='RK45')

# Afficher les valeurs de t et y
print(sol.t)
print(sol.y)

# Graphique de la solution
plt.plot(sol.t, sol.y[0])
plt.xlabel('t')
plt.ylabel('y')
plt.title('Solution de l\'équation différentielle')
plt.grid()
plt.show()

Bonsoir

Une approche mathématique possible :

Si on note avec

l'équation différentielle s'écrit

et donc

qui s'intègre en où est une primitive de sur un intervalle convenable ,

selon Sauro l'angle varie entre 0° et 45° donc doit au moins contenir le segment


on peut donner analytiquement connaissant les valeurs des constantes et


Je ne connais pas le phénomène physique dont l'étude mène à cette équation différentielle


c'est à Sauro de le préciser ainsi que la valeur des constantes et les conditions initiales (pour calculer les constantes d'intégration).


Ainsi les solutions (fonction d'une variable ) qui croit strictement (ou décroit strictement) sur un intervalle non trivial doivent vérifier :


ou .


Dans les deux cas, est une bijection de dans l'intervalle et on se ramène à l'une des deux équations :


ou


et ainsi une seconde intégration (donc une seconde constante d'intégration) permet de déterminer et par suite _{sauf erreur de ma part bien entendu}

Une petite étourderie, lire plutôt