Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieur AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau école ingénieur
Partager :

Méthode du simplexe 1

Posté par
Mathes1 06-01-24 à 21:09

Bonjour à tous
J'ai un exercice merci beaucoup d'avance
En utilisant l'algorithme du simplexe, résoudre le  programme suivant:
(PL)\begin{cases} \text{Max}z=-2x_1+6x_2+16x_3+x_5 \\ -2x_1+x_2+x_3+x_4-x_5\leq 6\\ x_2+x_3+x_4\leq 4\\ -x_1+x_3+4x_5\leq 8\\ x_i\geq 0, i=1,..,5 \end{cases}
la forme standard correspondante
\begin{cases} -2x_1+x_2+x_3+x_4-x_5+x_6=6\\ x_2+x_3+x_4+x_7=4\\ -x_1+x_3+4x_5+x_8=8\\ x_i\geq 0 ,i=1,..,8\end{cases}
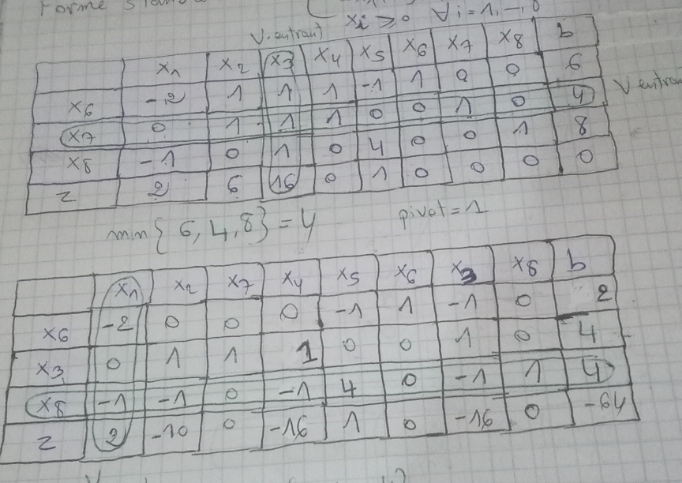
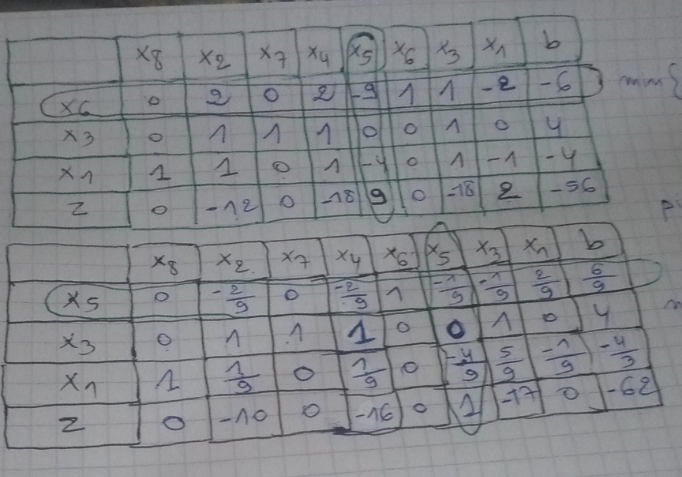
Méthode du simplexe 1
Méthode du simplexe 1
Merci beaucoup d'avance

Posté par
MattZolotarevre : Méthode du simplexe 1 07-01-24 à 00:37

Bonjour, sauf erreur de ma part, en posant, pour t\in\mathbb{R}_+,

x_1=-1+\dfrac{1}{2}t,
x_2=-3-\dfrac{1}{2}t,
x_3=7+\dfrac{1}{2}t,
x_4=0,
x_5=0,

ces x_i,\ i\in [\![1,5]\!] vérifient les contraintes et on a

-2x_1+6x_2+16x_3+x_5=96+4t.

Cette quantité peut être arbitrairement grande...

Posté par
MattZolotarevre : Méthode du simplexe 1 07-01-24 à 00:40

Oups, je raconte absolument n'importe quoi ! Message à ignorer totalement ! J'oubliais qu'il fallait que les x_i soient eux aussi positifs
Il est l'heure d'aller se coucher héhé.

Posté par
Mathes1re : Méthode du simplexe 1 07-01-24 à 12:57

Bonjour à tous,
est ce que ma méthode est juste?
merci à tous

Posté par
alb12re : Méthode du simplexe 1 07-01-24 à 13:50

Salut,
Je ne suis pas compétent pour corriger ta copie mais peux tu indiquer le maximum que tu as trouvé ?

Posté par
phyelec78re : Méthode du simplexe 1 07-01-24 à 14:19

Bonjour,

L'esprit de la méthode me semble respecté. Mais vos calculs pour le pivot de Gauss ne sont pas détaillés. Donc difficile de savoir si vos calculs sont bons.

Posté par
Mathes1re : Méthode du simplexe 1 07-01-24 à 14:29

bonjour
le problème est que je trouve pas tous les coefficients de z négatives ou nulle il y a un coefficient de z positif
Merci à tous

Posté par
Mathes1re : Méthode du simplexe 1 07-01-24 à 21:09

Bonjour
Il faut arrêter au 2ème tableau car on n'églige la valeur négatif de la variable de sortie lorsqu'on calcule le min [b/x1) dans ce cas
Merci beaucoup

Posté par
phyelec78re : Méthode du simplexe 1 07-01-24 à 22:50

dans votre premier tableau. dernière ligne (z) Il y a ( à mon avis une erreur): la première valeur est -2

Posté par
Mathes1re : Méthode du simplexe 1 07-01-24 à 23:00

Bonjour
Je suis désolé

Citation :
(PL)\begin{cases} \text{Max}z=2x_1+6x_2+16x_3+x_5 \\ -2x_1+x_2+x_3+x_4-x_5\leq 6\\ x_2+x_3+x_4\leq 4\\ -x_1+x_3+4x_5\leq 8\\ x_i\geq 0, i=1,..,5 \end{cases}
la forme standard correspondante
\begin{cases} 2x_1+x_2+x_3+x_4-x_5+x_6=6\\ x_2+x_3+x_4+x_7=4\\ -x_1+x_3+4x_5+x_8=8\\ x_i\geq 0 ,i=1,..,8\end{cases}

Posté par
Mathes1re : Méthode du simplexe 1 07-01-24 à 23:04

Bonjour
La solution optimale est infinie puisque la dernière  ligne du tableau du simplexe (2eme tableau) contient un coefficient positive (2) pour laquelle la colonne associé à 2 est constitué de valeurs négatifs ou nulle (-2,0,-1) dans un telle cas
Merci beaucoup


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !